题目内容
已知圆C与y轴相切,圆心在直线x-3y=0上,且在直线y=x上截得的弦长2 .求 圆C的方程.
.求 圆C的方程.

解析

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
双曲线 的虚轴长等于( )
的虚轴长等于( )
A.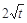 | B.-2t | C. | D.4 |
题目内容
已知圆C与y轴相切,圆心在直线x-3y=0上,且在直线y=x上截得的弦长2 .求 圆C的方程.
.求 圆C的方程.

解析

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案双曲线 的虚轴长等于( )
的虚轴长等于( )
A.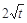 | B.-2t | C. | D.4 |