题目内容
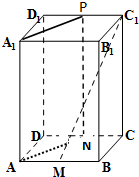 正四棱柱ABCD-ABC1D1(底面是正方形,侧棱与底面垂直)底面边长为1,高为2,M、N、P分别为线段AB、CD、C1D1的中点.
正四棱柱ABCD-ABC1D1(底面是正方形,侧棱与底面垂直)底面边长为1,高为2,M、N、P分别为线段AB、CD、C1D1的中点.(1)求证:MC1∥平面ANPA1;
(2)求异面直线CD与MC1所成角的大小的正切值.
分析:(1)连接PA,先证明四边形AMC1P是平行四边形,由此能够证明MC1∥平面ANPA1.
(2)由CD∥AB,知∠C1MB或其补角为导面直线CD与MC1所成的角.由此能求出异面直线CD与MC1所成角的正切值.
(2)由CD∥AB,知∠C1MB或其补角为导面直线CD与MC1所成的角.由此能求出异面直线CD与MC1所成角的正切值.
解答:解:(1)连接PA,
∵正四棱柱ABCD-ABC1D1中,M、P分别为线段AB、C1D1的中点,
∴AM
PC1,
∴四边形AMC1P是平行四边形,
∴MC1∥AP,
∵AP?平面ANPA1,MC1?平面ANPA1,
∴MC1∥平面ANPA1.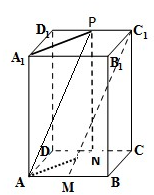
(2)∵CD∥AB,所以∠C1MB或其补角为导面直线CD与MC1所成的角.
连接BC1,∵AB⊥平面BCC1B,∴AB⊥BC1,
在Rt△MBC1中,BC1=
=
,MB=
,
∴tan∠C1MB=
=2
,
故异面直线CD与MC1所成角的大小的正切值为2
.
∵正四棱柱ABCD-ABC1D1中,M、P分别为线段AB、C1D1的中点,
∴AM
| ∥ |
. |
∴四边形AMC1P是平行四边形,
∴MC1∥AP,
∵AP?平面ANPA1,MC1?平面ANPA1,
∴MC1∥平面ANPA1.

(2)∵CD∥AB,所以∠C1MB或其补角为导面直线CD与MC1所成的角.
连接BC1,∵AB⊥平面BCC1B,∴AB⊥BC1,
在Rt△MBC1中,BC1=
| 4+1 |
| 5 |
| 1 |
| 2 |
∴tan∠C1MB=
| ||
|
| 5 |
故异面直线CD与MC1所成角的大小的正切值为2
| 5 |
点评:本题考查直线与平面平行的证明,考查异面直线所成角的正切值的求法,解决此类问题的关键是熟练掌握几何体的结构特征与几何体的线段长度关系,进而解决线面平行与垂直问题,异面直线所成角等问题.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
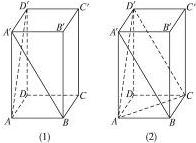 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是