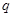题目内容
已知数列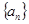 的前
的前 项和
项和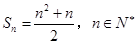 .
.
(1)求数列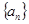 的通项公式;
的通项公式;
(2)设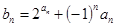 ,求数列
,求数列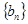 的前
的前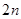 项和.
项和.
(1)  (2)
(2) 
解析试题分析:(1)题目已知 之间的关系,令
之间的关系,令 ,利用
,利用 ,即可求的
,即可求的 的值,令
的值,令 ,利用
,利用 与前n项和之间的关系
与前n项和之间的关系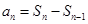 即可得到
即可得到 ,令
,令 检验首项即可得到
检验首项即可得到 的通项公式.
的通项公式.
(2)把(1)得到的通项公式代入 可以得到
可以得到 是由等比数列
是由等比数列 ,数列
,数列 之和,才用分组求和法,首先利用等比数列前n项和公式求的等比数列
之和,才用分组求和法,首先利用等比数列前n项和公式求的等比数列 的前n项和,再利用
的前n项和,再利用 对数列
对数列 进行分组
进行分组 即可求的数列
即可求的数列 的前n项和
的前n项和
(1)当 时,
时, ;
;
当 时,
时,
检验首项 符合
符合 ,所以数列
,所以数列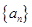 的通项公式为
的通项公式为 .
.
(2)由(1)可得 ,记数列
,记数列 的前
的前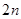 项和为
项和为 ,
,
则


故数列 的前
的前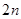 项和为
项和为
考点:数列前 项和 等差数列 等比数列 分组求和法
项和 等差数列 等比数列 分组求和法

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 满足
满足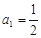 ,
,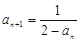
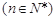 .
.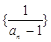 为等差数列,并求出
为等差数列,并求出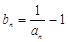 ,数列
,数列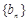 的前
的前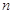 项和为
项和为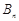 ,对任意
,对任意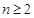 都有
都有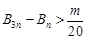 成立,求整数
成立,求整数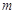 的最大值.
的最大值.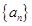 的前
的前 项和为
项和为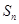 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得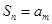 ,则称
,则称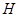 数列”.
数列”.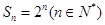 ,证明:
,证明: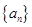 是等差数列,其首项
是等差数列,其首项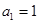 ,公差
,公差 ,若
,若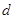 的值;
的值;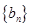 和
和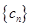 ,使得
,使得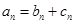
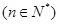 成立.
成立. 中,
中,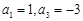 .
.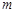 项和
项和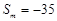 ,求
,求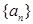 满足
满足 .
.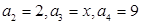 ,求
,求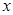 的取值范围;
的取值范围;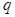 等比数列,
等比数列,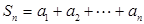 ,
,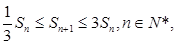 求
求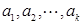 成等差数列,且
成等差数列,且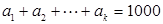 ,求正整数
,求正整数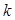 的最大值,以及
的最大值,以及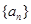 是等差数列,
是等差数列,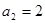 ,前四项和
,前四项和 。
。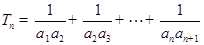 ,计算
,计算 。
。 为等差数列
为等差数列 的前
的前 项和,
项和,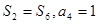 ,求
,求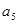 ;
; ,求首项
,求首项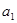 和公比
和公比