题目内容
5.已知O为坐标原点,双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线l:x=$\frac{{a}^{2}}{c}$与双曲线的一条渐近线交于点A,且△OAF的面积为$\frac{{a}^{2}}{2}$,则该双曲线的两条渐近线的夹角大小为90°.分析 据条件设出点A 的坐标,利用△OAF的面积(O为原点),找出a与b的关系,得到渐近线的斜率,进而得到倾斜角,从而得到结果.
解答 解:双曲线的渐近线方程是:y=±$\frac{b}{a}$x,右准线方程为x=$\frac{{a}^{2}}{c}$,
∵右准线与一条渐近线交于点A,
可设点A($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
∵△OAF的面积为$\frac{{a}^{2}}{2}$,(O为原点),
∴$\frac{1}{2}$c•$\frac{ab}{c}$=$\frac{{a}^{2}}{2}$,∴$\frac{b}{a}$=1,
∴渐近线的斜率分别为1和-1,
∴两条渐近线的倾斜角分别为45°,135°,
∴该双曲线的两条渐近线的夹角为90°.
故答案为:90°.
点评 本题考查双曲线的方程和性质,考查直线的斜率和两直线的夹角问题,考查三角形的面积计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.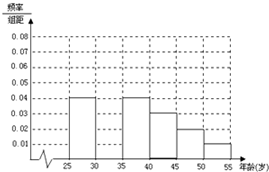 某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
(一)人数统计表:
(二)各年龄段人数频率分布直方图:
(Ⅰ)在答题卡给定的坐标系中补全频率分布直方图,并求出n、p、a的值;
(Ⅱ)从[40,50]岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动.若将这6个人通过抽签分成甲、乙两组,每组的人数相同,求[45,50]岁中被抽取的人恰好又分在同一组的概率;
(Ⅲ)根据所得各年龄段人数频率分布直方图,估计在本地[25,55]岁的人群中“低碳族”年龄的中位数.
 某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.
某班同学利用春节进行社会实践,对本地[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图.| 序号 | 分组 | 本组“低碳族”的人数 | “低碳族”人数在本组中所占的比例 |
| 1 | [25,30) | 120 | 0.6 |
| 2 | [30,35) | 195 | p |
| 3 | [35,40) | 100 | 0.5 |
| 4 | [40,45) | a | 0.4 |
| 5 | [45,50) | 30 | 0.3 |
| 6 | [50,55] | 15 | 0.3 |
(二)各年龄段人数频率分布直方图:
(Ⅰ)在答题卡给定的坐标系中补全频率分布直方图,并求出n、p、a的值;
(Ⅱ)从[40,50]岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动.若将这6个人通过抽签分成甲、乙两组,每组的人数相同,求[45,50]岁中被抽取的人恰好又分在同一组的概率;
(Ⅲ)根据所得各年龄段人数频率分布直方图,估计在本地[25,55]岁的人群中“低碳族”年龄的中位数.
14.已知△ABC中,a,b,c分别是角A,B,C的对边,a=$\sqrt{2}$,b=$\sqrt{3}$,A=45°,则B=( )
| A. | 60° | B. | 120° | C. | 60°或120° | D. | 90° |
15.若函数f(x)=x3-tx2+3x在区间[1,4]上单调递减,则实数t的取值范围是( )
| A. | (-∞,$\frac{51}{8}$] | B. | (-∞,3] | C. | [$\frac{51}{8}$,+∞) | D. | [3,+∞) |