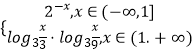题目内容
【题目】已知集合A={x|2﹣a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若A∩B=,求实数a的取值范围.
【答案】
(1)解:当a=3时,A={x|2﹣a≤x≤2+a}={x|﹣1≤x≤5},B={x|x≤1或x≥4}.
则A∩B={x|﹣1≤x≤1或4≤x≤5}
(2)解:若2+a<2﹣a,即a<0时,A=,满足A∩B=,
若a≥0,若满足A∩B=,
则 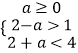 ,即
,即 ![]() ,解得0≤a<1
,解得0≤a<1
综上实数a的取值范围a<1
【解析】(1)当a=3时,根据集合的基本运算即可求A∩B;(2)若A∩B=,建立条件关系即可求实数a的取值范围.
【考点精析】利用集合的交集运算对题目进行判断即可得到答案,需要熟知交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产![]() 个机器人模型,并对生产的机器人进行编号:
个机器人模型,并对生产的机器人进行编号: ![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的机器人样本,试验小组对
的机器人样本,试验小组对![]() 个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
分组 | 机器人数 | 频率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)补全频率分布表,画出频率分布直方图;
(2)若随机抽的第一个号码为![]() ,这
,这![]() 个机器人分别放在
个机器人分别放在![]() 三个房间,从
三个房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,求
房间,求![]() 房间被抽中的人数是多少?
房间被抽中的人数是多少?
(3)从动作个数不低于![]() 的机器人中随机选取
的机器人中随机选取![]() 个机器人,该
个机器人,该![]() 个机器人中动作个数不低于
个机器人中动作个数不低于![]() 的机器人记为
的机器人记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.