题目内容
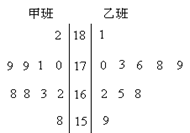
某班高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
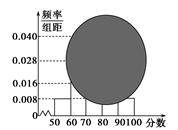
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
(1)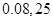 ;(2)
;(2) ;(3)
;(3)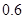 .
.
解析试题分析:(1)由频率分布直方图可知分数在[50,60)的频率为0.008×10=0.08,再由茎叶图知分数在[50,60)之间的频数为2,则全班人数为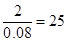 ;(2)[80,90)之间的人数为
;(2)[80,90)之间的人数为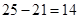 人,根据对应的频率为
人,根据对应的频率为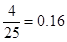 ,所以矩形的高为
,所以矩形的高为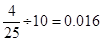 ;(3)根据列举法能够知道在[80,100]之间的试卷中任取两份的基本事件15个,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是
;(3)根据列举法能够知道在[80,100]之间的试卷中任取两份的基本事件15个,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是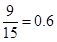 .
.
试题解析:(1)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知:分数在[50,60)之间的频数为2,
所以全班人数为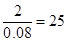 .
.
(2)由(1)知,分数在[80,90)之间的人数为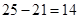 人. 则对应的频率为
人. 则对应的频率为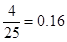 ,所以[80,90)间的矩形的高为
,所以[80,90)间的矩形的高为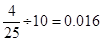 .
.
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.其中,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是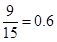 .
.
考点:1.对频率分布直方图和茎叶图的认识;2.古典概型的应用.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案衡水某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| | 60分 以下 | 61~ 70分 | 71~ 80分 | 81~ 90分 | 91~ 100分 |
| 甲班 (人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班 (人数) | 4 | 8 | 13 | 15 | 10 |
(1)试分别估计两个班级的优秀率.
(2)由以上统计数据填写下面2×2列联表,并判断“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”是否有帮助?
| | 优秀人数 | 非优秀人数 | 总计 |
| 甲班 | | | |
| 乙班 | | | |
| 总计 | | | |
 ,
,
某工厂生产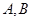 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
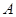 | 7 | 7 | 7.5 | 9 | 9.5 |
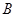 | 6 | 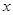 | 8.5 | 8.5 |  |
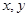 看不清,统计员只记得
看不清,统计员只记得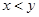 ,且
,且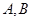 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
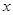 与
与 的值;
的值;(Ⅱ)若从被检测的5件
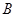 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.


 名学生被考官L面试,求
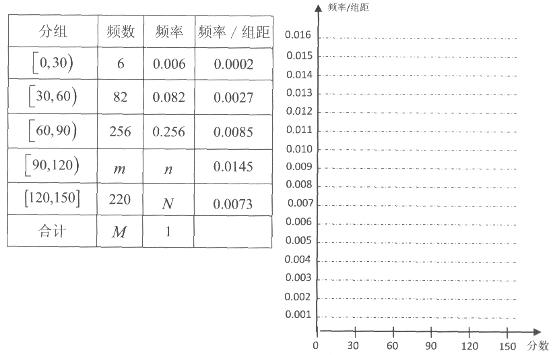
名学生被考官L面试,求 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
 天数据,记
天数据,记 表示抽到
表示抽到 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.