题目内容
 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即 日均值在
日均值在 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米
微克/立方米 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在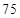 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 监测数据中随机的抽取
监测数据中随机的抽取 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
(1)在这 天的
天的 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这 天的数据中任取
天的数据中任取 天数据,记
天数据,记 表示抽到
表示抽到 监测数据超标的天数,求
监测数据超标的天数,求 的分布列及数学期望;
的分布列及数学期望;
(3)以这 天的
天的 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.
(1)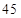 ;(2)详见解析;(3)
;(2)详见解析;(3)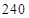 .
.
解析试题分析:(1)根据茎叶图中的信息,将数据按一定的顺序(由大到小或由小到大)依次进行排列,然后取相应的中位数即可;(2)先确定 天中空气质量超标的天数以及补超标的天数,然后利用超几何分布列举出随机变量
天中空气质量超标的天数以及补超标的天数,然后利用超几何分布列举出随机变量 的概率分布列,并求出随机变量
的概率分布列,并求出随机变量 的数学期望;(3)先根据
的数学期望;(3)先根据 天中空气质量达到一级或二级的天数,求出相应的概率,然后利用二项分布的计算公式求出相应的均值.
天中空气质量达到一级或二级的天数,求出相应的概率,然后利用二项分布的计算公式求出相应的均值.
试题解析:(1)由茎叶图可得中位数是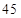 ;
;
(2)依据条件, 服从超几何分布:其中
服从超几何分布:其中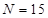 ,
,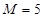 ,
,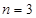 ,
, 的可能值为
的可能值为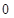 、
、 、
、 ,
,
由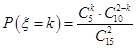 ,
,
得 ,
, 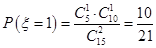 ,
,  ,
,
所以 的分布列为:
的分布列为:
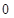


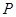
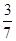
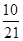
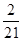
 ;
;
(3)依题意可知,一年中每天空气质量达到一级或二级的概率为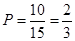 ,
,
一年中空气质量达到一级或二级的天数为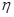 ,则
,则 ,
, ,
,
所以,一年中平均有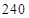 天的空气质量达到一级或二级.
天的空气质量达到一级或二级.
考点:1.茎叶图;2.中位数;3.超几何分布;4.离散型随机变量的分布列与期望;5.二项分布

2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附:


 .
.
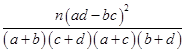 ,其中n=a+b+c+d)
,其中n=a+b+c+d) t该产品获利润
t该产品获利润 元,未售出的产品,每
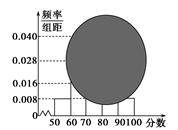
元,未售出的产品,每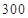 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t,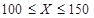 )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,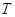 (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。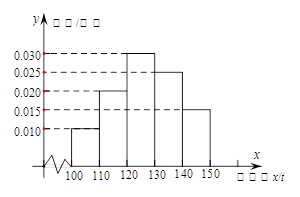
 不少于57000元的概率;
不少于57000元的概率; ,则取
,则取 ,且
,且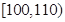 的概率),求利润
的概率),求利润
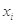 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得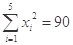 ,
, ,
, ,
,  .
.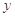 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
; ,
, ,其中
,其中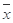 ,
, 为
为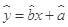 .
.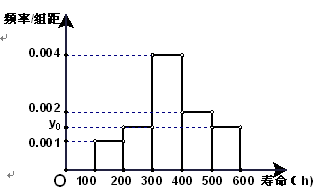
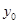 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原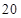 个元件,寿命为
个元件,寿命为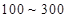 之间的应抽取几个;
之间的应抽取几个; 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为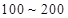 ,一个寿命为
,一个寿命为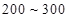 ”的概率.
”的概率.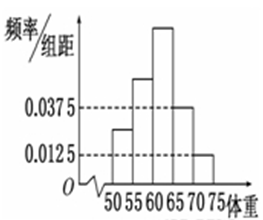
 ,第2组
,第2组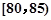 ,第3组
,第3组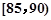 ,第4组
,第4组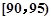 ,第5组
,第5组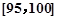 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.