题目内容
如图1,已知四边形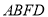 为直角梯形,
为直角梯形,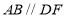 ,
,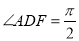 ,
, ,
, 为等边三角形,
为等边三角形,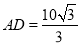 ,
, ,如图2,将
,如图2,将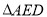 ,
, 分别沿
分别沿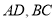 折起,使得平面
折起,使得平面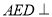 平面
平面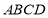 ,平面
,平面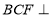 平面
平面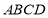 ,连接
,连接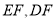 ,设
,设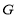 为
为 上任意一点.
上任意一点.

(1)证明: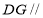 平面
平面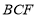 ;
;
(2)若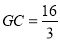 ,求
,求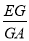 的值.
的值.
练习册系列答案
相关题目
题目内容
如图1,已知四边形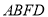 为直角梯形,
为直角梯形,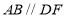 ,
,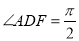 ,
, ,
, 为等边三角形,
为等边三角形,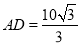 ,
, ,如图2,将
,如图2,将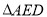 ,
, 分别沿
分别沿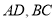 折起,使得平面
折起,使得平面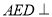 平面
平面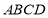 ,平面
,平面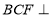 平面
平面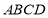 ,连接
,连接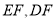 ,设
,设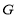 为
为 上任意一点.
上任意一点.

(1)证明: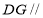 平面
平面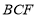 ;
;
(2)若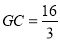 ,求
,求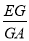 的值.
的值.