题目内容
【题目】汕头市有一块如图所示的海岸,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:
角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:
方案l:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() ,用长度为
,用长度为![]() 的围网依托岸边围成三角形
的围网依托岸边围成三角形![]() (
(![]() 为围网).
为围网).
方案2:在![]() 的平分线上取一点
的平分线上取一点![]() ,再从岸边
,再从岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() ,使得
,使得![]() ,用长度为
,用长度为![]() 的围网依托岸边围成四边形
的围网依托岸边围成四边形![]() (
(![]() ,
,![]() 为围网).
为围网).
记三角形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() . 请分别计算
. 请分别计算![]() ,
,![]() 的最大值,并比较哪个方案好.
的最大值,并比较哪个方案好.
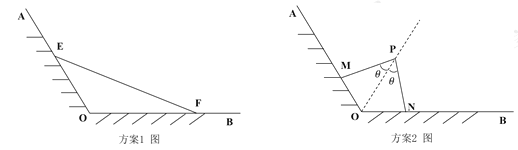
【答案】方案2好.
【解析】
方案1中,利用余弦定理和基本不等式求出面积最值,方案2中,利用正弦定理和三角函数的性质求出面积最值,然后比较大小,即可得哪种方案好.
解: 方案1:设![]() ,
,![]() ,
,
在![]() 中,由余弦定理得:
中,由余弦定理得:![]() ,
,
即![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
∴![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
∴![]() 最大值为
最大值为![]() .
.
方案2: 在![]() 中,由正弦定理得:
中,由正弦定理得:![]() 即
即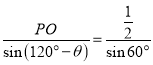 ,
,
∴![]() ,
,
∴![]()


![]()
(当且仅当![]() 时等号成立)
时等号成立)
∴![]() 最大值为
最大值为![]() ,
,
∵![]() ,∴方案2好.
,∴方案2好.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目