题目内容
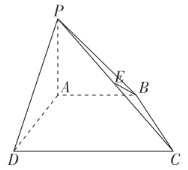
【题目】如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且
．
（Ⅰ）求证：CD⊥平面PAD；
（Ⅱ）求二面角F–AE–P的余弦值；
（Ⅲ）设点G在PB上，且
．判断直线AG是否在平面AEF内，说明理由．
【答案】(Ⅰ)见解析；
(Ⅱ) 
；
(Ⅲ)见解析.
【解析】
(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；
(Ⅱ)建立空间直角坐标系，结合两个半平面的法向量即可求得二面角F-AE-P的余弦值；
(Ⅲ)首先求得点G的坐标，然后结合平面
的法向量和直线AG的方向向量可判断直线是否在平面内.
(Ⅰ)由于PA⊥平面ABCD，CD
平面ABCD，则PA⊥CD，
由题意可知AD⊥CD，且PA∩AD=A，
由线面垂直的判定定理可得CD⊥平面PAD.
(Ⅱ)以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD,AP方向为y轴，z轴建立如图所示的空间直角坐标系
，
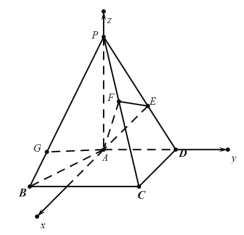
易知：
，
由
可得点F的坐标为
，
由
可得
，
设平面AEF的法向量为：
，则
，
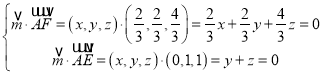据此可得平面AEF的一个法向量为：
，
很明显平面AEP的一个法向量为
，
，
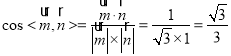二面角F-AE-P的平面角为锐角，故二面角F-AE-P的余弦值为.
(Ⅲ)易知
，由
可得
，
则
，
注意到平面AEF的一个法向量为：，
其
且点A在平面AEF内，故直线AG在平面AEF内.
练习册系列答案
相关题目
