题目内容
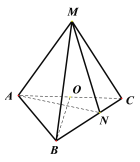
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点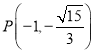 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)根据椭圆定义求出![]() ,即可求出椭圆
,即可求出椭圆![]() 的标准方程;
的标准方程;
(2)假设满足条件的直线![]() 存在,与椭圆方程联立,求出直线
存在,与椭圆方程联立,求出直线![]() 满足的条件,根据已知条件
满足的条件,根据已知条件![]() 在线段
在线段![]() 的垂直平分线上,结合直线的斜率公式,推导出直线
的垂直平分线上,结合直线的斜率公式,推导出直线![]() 不存在.
不存在.
(1)因为椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,
所以![]() .由椭圆定义可得
.由椭圆定义可得 ,
,
解得![]() ,所以
,所以![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)假设存在满足条件的直线![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
由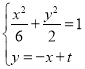 得
得![]() ,即
,即
![]() ,
,
![]() ,
,
解得![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由于![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
所以![]() 又
又![]() ,
,
所以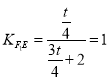 ,解得
,解得![]() .
.
当![]() 时,不满足
时,不满足![]() .
.
所以不存在满足条件的直线![]() .
.

【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.