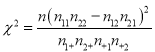题目内容
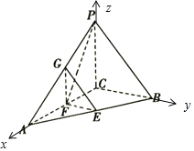
【题目】如图,三棱锥![]() 中,
中,![]() 两两垂直,
两两垂直,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:平面![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由中位线定理证得![]() ,由线面平行的判定定理说明
,由线面平行的判定定理说明![]() 平面
平面![]() ,同理可证
,同理可证![]() 平面
平面![]() ,再由面面平行的判定定理说明平面
,再由面面平行的判定定理说明平面![]() 面
面![]() ;
;
(2)由三棱锥![]() 中,
中,![]() 两两垂直,即可以
两两垂直,即可以![]() 为坐标原点,以
为坐标原点,以![]() 为坐标轴建立空间直角坐标系,分别表示点P,A,B,F的坐标,进而求得
为坐标轴建立空间直角坐标系,分别表示点P,A,B,F的坐标,进而求得![]() 与面
与面![]() 的法向量,设
的法向量,设![]() 与面
与面![]() 所成角为
所成角为![]() ,由
,由![]() 算得答案.
算得答案.
(1)证明:∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
同理可得:![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,以
为坐标原点,以![]() 为坐标轴建立空间直角坐标系如图所示:
为坐标轴建立空间直角坐标系如图所示:
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则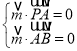 ,
,
∴![]() ,令
,令![]() 可得
可得![]() .
.
∴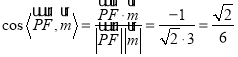 .
.
设![]() 与面
与面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
∴![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 阅读快车系列答案
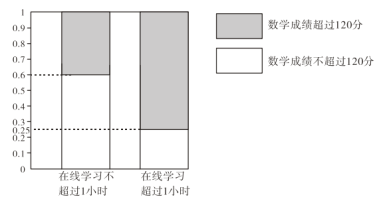
阅读快车系列答案【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
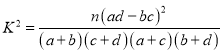
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |