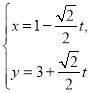题目内容
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
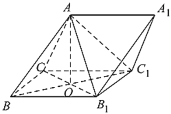
(1)求证:![]() ;
;
(2)若![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先由![]() 平面
平面![]() 证得
证得![]() ,根据四边形
,根据四边形![]() 是菱形证得
是菱形证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得
,进而证得![]() .
.
(2)首先根据“直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ”得到
”得到![]() .以
.以![]() 为坐标原点建立空间直角坐标系,通过平面
为坐标原点建立空间直角坐标系,通过平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
(1)证明:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以四边形
,所以四边形![]() 是菱形,所以
是菱形,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
(2)因为![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() ,
,
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
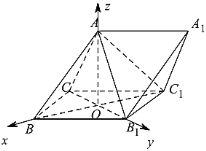
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为![]()
![]() ,
,
所以![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则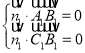 ,即
,即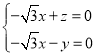 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以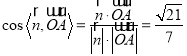 ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]()