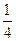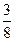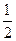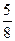题目内容
(本小题满分12分)
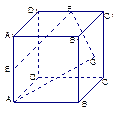
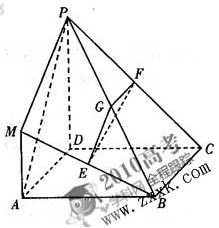
在如图所示的几何体中,四边形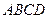 是正方形,
是正方形,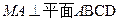 ,
,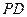
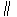
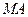 ,
,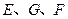 分别为
分别为
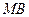 、
、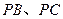 的中点,且
的中点,且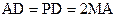 .
.
(Ⅰ) 求证:平面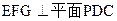 ;
;
(Ⅱ)求三棱锥 .
.
在如图所示的几何体中,四边形
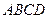 是正方形,
是正方形,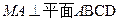 ,
,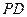
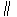
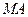 ,
,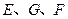 分别为
分别为
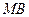 、
、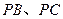 的中点,且
的中点,且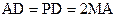 .
.
(Ⅰ) 求证:平面
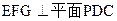 ;
;(Ⅱ)求三棱锥
 .
.(Ⅰ)证明见解析
( Ⅱ )1:4
( Ⅱ )1:4
本题考查了空间几何体的线面与面面垂直的性质与判定以及几何体的体积计算等问题,考查了同学们的识图能力以及空间想象能力以及计算能力。
(I)证明:由已知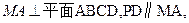
所以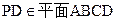
又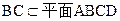 ,
,
所以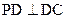
因为 四边形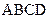 为正方形,
为正方形,
所以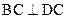 ,
,
又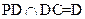 ,
,
因此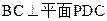 ---------------------------------------------------
---------------------------------------------------
在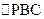 中,因为
中,因为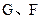 分别为
分别为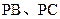 的中点,
的中点,
所以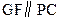
因此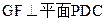
又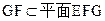 ,
,
所以 .
.
(Ⅱ)解:因为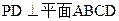 ,四边形
,四边形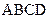 为正方形,不妨设
为正方形,不妨设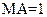 ,
,
则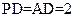 ,
,
所以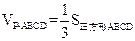 ·
·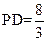
由于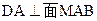 的距离,且
的距离,且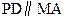
所以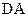 即为点
即为点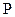 到平面
到平面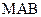 的距离,
的距离,
三棱锥
所以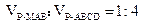
(I)证明:由已知
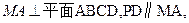
所以
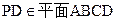
又
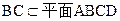 ,
,所以
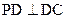
因为 四边形
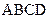 为正方形,
为正方形,所以
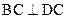 ,
,又
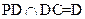 ,
,因此
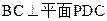 ---------------------------------------------------
---------------------------------------------------在
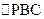 中,因为
中,因为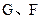 分别为
分别为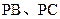 的中点,
的中点,所以
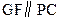
因此
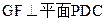
又
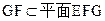 ,
,所以
 .
.(Ⅱ)解:因为
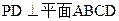 ,四边形
,四边形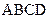 为正方形,不妨设
为正方形,不妨设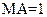 ,
,则
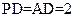 ,
,所以
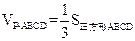 ·
·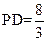
由于
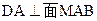 的距离,且
的距离,且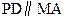
所以
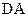 即为点
即为点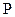 到平面
到平面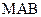 的距离,
的距离,三棱锥

所以
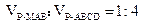

练习册系列答案
相关题目
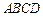 和矩形
和矩形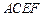 所在的平面互相垂直,
所在的平面互相垂直,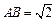 ,AF = 1,M是线段
,AF = 1,M是线段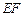 的中点.
的中点.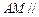 平面
平面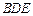 ;
;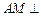 平面
平面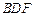 ;
;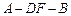 的大小.
的大小.
 的棱长为1,点
的棱长为1,点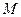 是棱
是棱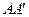 的中点,点
的中点,点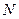 是棱
是棱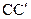 的中点,点
的中点,点 是上底面
是上底面 的中心.
的中心.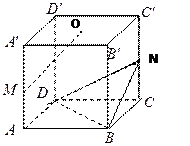 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;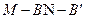 的大小;
的大小;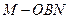 的体积.
的体积.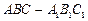 的底面正三角形的边长是2,D是
的底面正三角形的边长是2,D是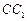 的中点,直线
的中点,直线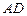 与侧面
与侧面 所成的角是
所成的角是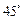 .
.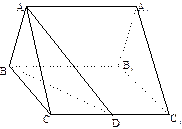
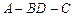 的大小;
的大小;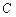 到平面
到平面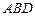 的距离.
的距离.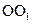 内有一个三棱柱
内有一个三棱柱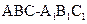 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。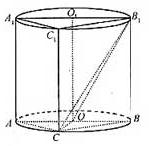
 平面
平面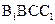 ;
;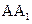 ,在圆柱
,在圆柱 。
。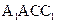 与平面
与平面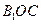 所成的角为
所成的角为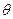
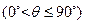 ,当
,当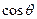 的值。
的值。 平行
平行  垂直
垂直  相交
相交 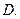 异面
异面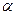 和两条直线a、b,则下列命题中正确的是
和两条直线a、b,则下列命题中正确的是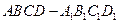 中,
中,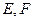 分别为棱
分别为棱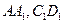 的中点,
的中点,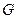 是侧面
是侧面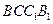 的中心,则空间四边形
的中心,则空间四边形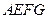 在正方体的六个面上的射影图形面积的最大值是( )
在正方体的六个面上的射影图形面积的最大值是( )