题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
,![]() 的解析式;
的解析式;
(3)若函数![]() ,
,![]() ,求函数
,求函数![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)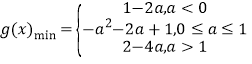 。
。
【解析】
(1)根据题意,由偶函数的性质结合二次函数的性质分析可得答案;
(2)设x>0,结合函数的奇偶性,从而得到函数的解析式;
(3)先求出g(x)的表达式,求出对称轴,通过讨论对称轴的位置,得到函数g(x)的最值
(1)根据题意,f(x)的增区间为(﹣1,0)、(1,+∞);
(2)根据题意,设x<0,则﹣x>0,
又由f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x2﹣2x,
f(x)=f(﹣x)=x2+2x;
故函数的解析式为f(x)=![]() ;
;
(3)由(2)可得当x∈[1,2],f(x)=x2﹣2x,
则g(x)=f(x)﹣2ax+2=x2﹣2(a+1)x+2,
对称轴方程为:x=a+1,
①当a+1≤1时,g(x)min=g(1)=1﹣2a为最小;
②当1<a+1≤2时,g(x)min=g(a+1)=﹣a2﹣2a+1为最小;
③当a+1>2时,g(x)min=g(2)=2﹣4a为最小
故g(x)=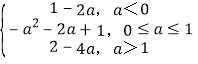 .
.

练习册系列答案
相关题目