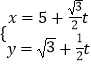题目内容
【题目】已知f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=3x .
(1)求 f(x),g(x);
(2)若对于任意实数t∈[0,1],不等式f(2t)+ag(t)<0恒成立,求实数a的取值范围;
(3)若存在m∈[﹣2,﹣1],使得不等式af(m)+g(2m)<0成立,求实数a的取值范围.
【答案】
(1)解:∵f(x)、g(x)分别是奇函数、偶函数,
∴f(﹣x)=﹣f(x),g(﹣x)=g(x),
令x取﹣x,代入f(x)+g(x)=3x ①,
f(﹣x)+g(﹣x)=3﹣x,即﹣f(x)+g(x)=3﹣x ②,
由①②解得,f(x)= ![]() ,g(x)=
,g(x)= ![]()
(2)解:由(1)可得,不等式f(2t)+ag(t)<0为:
不等式 ![]() +a
+a ![]() <0,
<0,
化简得,(3t﹣3﹣t)+a<0,即a<﹣3t+3﹣t,
∵任意实数t∈[0,1],不等式f(2t)+ag(t)<0恒成立,
且函数y=﹣3t+3﹣t在[0,1]上递减,∴y≥ ![]() ,即a<
,即a< ![]()
则实数a的取值范围是(﹣∞, ![]() )
)
(3)解:由(1)可得,不等式af(m)+g(2m)<0为:
a ![]() +
+ ![]() <0,
<0,
∵m∈[﹣2,﹣1],∴ ![]() ,则化简得,
,则化简得,
a> ![]() =
= ![]() =
= ![]() ,
,
令t=3﹣m﹣3m,∵m∈[﹣2,﹣1],∴t∈[ ![]() ,
, ![]() ],
],
则a> ![]() ,
,
∴存在m∈[﹣2,﹣1],使得不等式af(m)+g(2m)<0成立等价于:
存在t∈[ ![]() ,
, ![]() ],使得不等式a>
],使得不等式a> ![]() 成立,
成立,
∵ ![]() =2
=2 ![]() ,当且仅当
,当且仅当 ![]() ,即t=
,即t= ![]() 时取等号,
时取等号,
∴函数y= ![]() 在[
在[ ![]() ,
, ![]() ]递增,则函数y=
]递增,则函数y= ![]() 的最小值是
的最小值是 ![]() ,
,
即a> ![]() ,故实数a的取值范围是(
,故实数a的取值范围是( ![]() ,+∞)
,+∞)
【解析】(1)将﹣x代入已知等式,利用函数f(x)、g(x)的奇偶性,得到关于f(x)与g(x)的又一个方程,将二者看做未知数解方程组,解得f(x)和g(x);(2)由(1)和t的范围化简不等式f(2t)+ag(t)<0,分离出a后构造函数,由指数函数的单调性求出最小值,根据恒成立求出实数a的取值范围;(3)由(1)和m的范围化简不等式af(m)+g(2m)<0,分离出a后构造函数,利用换元法法,由函数的单调性求出最小值,根据存在性问题求出实数a的取值范围;
【考点精析】掌握函数奇偶性的性质是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案