Question

【题目】在△ABC中，AC＝6，cos B＝ ，C＝ .

(1)求AB的长；

(2)求cos 的值．

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）由同角函数基本关系式得sin B＝，求出sin B＝；再由正弦定理求出. （2）由三角形三个内角和的关系得出A＝π－(B＋C)；再利用诱导公式求出cos A＝－cos Bcos ＋sin Bsin＝－；接着求出sin A＝＝；最后利用诱导公式求出cos＝cos Acos ＋sin A·sin＝.

试题解析：

(1)因为cos B＝ ，0<B<π，

所以sin B＝＝＝ ，

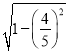由正弦定理知， ，

所以 .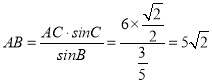

(2)在三角形ABC中A＋B＋C＝π，

所以A＝π－(B＋C)．

于是cos A＝－cos(B＋C)

＝－cos

＝－cos Bcos ＋sin Bsin，

又cos B＝ ，sin B＝ ，

故cos A＝－ × ＋ × ＝－ ，

因为0<A<π，所以sin A＝＝ .

因此cos ＝cos Acos ＋sin A·sin ＝－ × ＋ × ＝.

【点晴】

解三角形的常用的与三内角及三边有关的知识有：同角函数基本关系式、三个内角关系、正弦定理、余弦定理及其推论、三角形的面积公式等，这些公式一定要熟记才能做到灵活应用.