题目内容
【题目】下列命题中,正确的个数是（ ）
①直线上有两个点到平面的距离相等,则这条直线和这个平面平行；
②
为异面直线,则过
且与
平行的平面有且仅有一个；
③直四棱柱是直平行六面体；
④两相邻侧面所成角相等的棱锥是正棱锥.
A.0B.1C.2D.3
【答案】B
【解析】
①可通过点分居平面两侧来进行否定；
②利用异面直线的性质与线面平行的判定即可判断出②正确；
③通过直四棱柱和直平行六面体定义来进行否定；
④通过把正方形折叠的方式可找到反例来进行否定.
①中，两点可分别位于平面的两侧，存在到平面距离相等的情况，此时直线和平面相交
①错误；
②中，作
的平行线
，且与
交于一点；则由
可确定唯一的平面
，此时
，可知这样的平面有且仅有一个，②正确；
③中，直四棱柱为底面为四边形，侧棱垂直于底面的四棱柱；直平行六面体是底面为平行四边形，且侧棱垂直于底面的四棱柱；③错误；
④中，若正方形一个顶点为
，
为两边的中点，如下图所示：
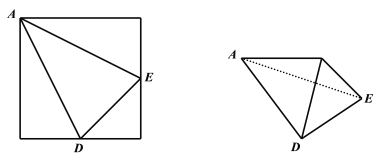
将正方形沿
三边折叠为三棱锥，满足两相邻侧面所成角相等，但不是正三棱锥
④错误
故选：
【题目】为满足人们的阅读需求，图书馆设立了无人值守的自助阅读区，提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况，数据统计如下（单位：本）.
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
（1）根据统计数据估计文学类图书分类正确的概率；
（2）根据统计数据估计图书分类错误的概率.
【题目】郴州某超市计划按月订购一种饮料，每天进货量相同，进货成本每瓶6元，售价每瓶8元，未售出的饮料降价处理，以每瓶3元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间
，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率．
（1）求六月份这种饮料一天的需求量X（单位：瓶）的分布列；
（2）设六月份一天销售这种饮料的利润为Y（单位：元），当六月份这种饮料一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？
