题目内容
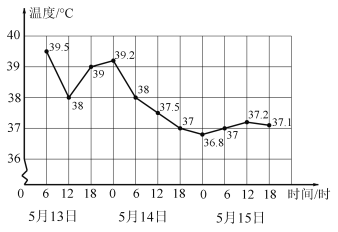
【题目】如图是一位发烧病人的体温记录折线图，下列说法不正确的是（ ）
A.病人在5月13日12时的体温是
B.病人体温在5月14日0时到6时下降最快
C.从体温上看，这个病人的病情在逐渐好转
D.病人体温在5月15日18时开始逐渐稳定
【答案】D
【解析】
根据折线统计图中的信息，对四个选项逐一分析即可得解.
对于A：由图可知，病人在5月13日12时的体温是
，故A正确；
对于B：从图中可以看出，5月13日6时到12时折线下降比其它时间段陡直，所以病人体温在5月13日6时到12时下降最快，故B正确；
对于C：从图中看，曲线整体呈现下降的趋势，则这个病人的病情是好转了，故C正确；
对于D：由图可知，病人体温从5月14日18时到5月15日18时比较稳定，在
上下浮动，故D不正确.
故选：D.
一线名师权威作业本系列答案【题目】著名物理学家李政道说：“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的，它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例，把八度分成13个半音，使相邻两个半音之间的频率比是常数，如下表所示，其中
表示这些半音的频率，它们满足
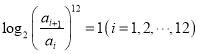.若某一半音与
的频率之比为
，则该半音为（ ）
频率 |
|
|
|
|
|
|
|
|
|
|
|
| |
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C（八度） |
A.
B.GC.
D.A
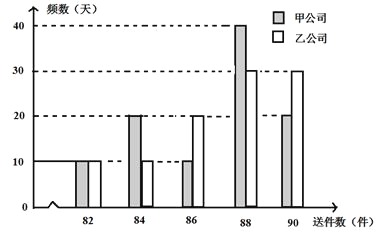
【题目】为了提高生产线的运行效率，工厂对生产线的设备进行了技术改造．为了对比技术改造后的效果，采集了生产线的技术改造前后各20次连续正常运行的时间长度（单位：天）数据，并绘制了如茎叶图：
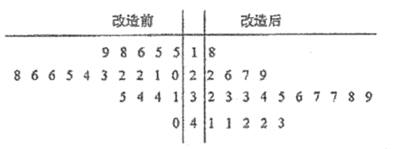
（1）（i）设所采集的40个连续正常运行时间的中位数m，并将连续正常运行时间超过m和不超过m的次数填入下面的列联表：
超过 | 不超过 | |
改造前 | ||
改造后 |
（ii）根据（i）中的列联表，能否有99%的把握认为生产线技术改造前后的连续正常运行时间有差异？
附：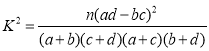
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）工厂的生产线的运行需要进行维护，工厂对生产线的生产维护费用包括正常维护费、保障维护费两种．对生产线设定维护周期为T天（即从开工运行到第kT天
进行维护．生产线在一个生产周期内设置几个维护周期，每个维护周期相互独立．在一个维护周期内，若生产线能连续运行，则不会产生保障维护费；若生产线不能连续运行，则产生保障维护费．经测算，正常维护费为0.5万元/次；保障维护费第一次为0.2万元/周期，此后每增加一次则保障维护费增加0.2万元．现制定生产线一个生产周期（以120天计）内的维护方案：
，
．以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率，求一个生产周期内生产维护费的分布列．
【题目】英国统计学家E．H．辛普森1951年提出了著名的辛普森悖论，下面这个案例可以让我们感受到这个悖论．有甲乙两名法官，他们都在民事庭和行政庭主持审理案件，他们审理的部分案件被提出上诉．记录这些被上述案件的终审结果如下表所示（单位：件）：
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
，
和
，记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
，
和
，则下面说法正确的是
A. 
，
，
B. ，，
C. 
，
，D. ，，
