题目内容
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:
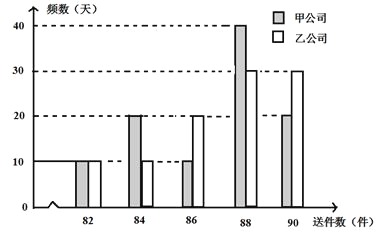
(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
【答案】(1)![]() ;(2)①分布列详见解析,数学期望为156.8元;②小王应当到甲公司应聘“快递员”的工作,理由详见解析.
;(2)①分布列详见解析,数学期望为156.8元;②小王应当到甲公司应聘“快递员”的工作,理由详见解析.
【解析】
(1)根据题意分![]() 与
与![]() 两段求出一日工资y(单位:元)与送件数n的函数关系即可.
两段求出一日工资y(单位:元)与送件数n的函数关系即可.
(2)①根据送件数以及(1)中的函数可知X的所有可能取值为152,154,156,158,160.在结合图中各送件数的频数求出对应的频率,继而求得分布列与数学期望即可.
②分别求出两家公司送餐日工资的数学期望,比较大小再判定即可.
(1)由题意:当![]() 时,
时,![]() 元;
元;
当![]() 时,
时,![]() .
.
∴乙公司的快递员一日工资y(单位:元)与送件数n的函数关系为:
![]()
(2)①X的所有可能取值为152,154,156,158,160.
由题可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴X的分布列为:
X | 152 | 154 | 156 | 158 | 160 |
P | 0.1 | 0.2 | 0.1 | 0.4 | 0.2 |
X的数学期望![]() (元)
(元)
②设乙公司的日工资为Y,
则![]() (元)
(元)
由于到甲公司的日工资的数学期望(均值)比乙公司的日工资的数学期望(均值)高,
所以小王应当到甲公司应聘“快递员”的工作.

 名校课堂系列答案
名校课堂系列答案【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为研究学生网上学习的情况,某校社团对男女各10名学生进行了网上在线学习的问卷调查,每名学生给出评分(满分100分),得到如图所示的茎叶图.
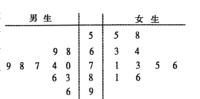
(1)根据茎叶图判断男生组和女生组哪个组对网课的评价更高?并说明理由;
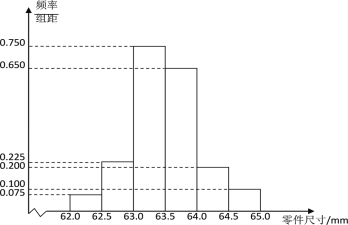
(2)如图是按该20名学生的评分绘制的频率分布直方图,求![]() 的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
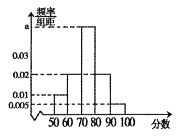
(3)求该20名学生评分的中位数![]() ,并将评分超过
,并将评分超过![]() 和不超过
和不超过![]() 的学生数填入下面的列联表:
的学生数填入下面的列联表:
超过 | 不超过 | |
男生 | ||
女生 |
根据列联表,能否有![]() 的把握认为男生和女生的评分有差异?
的把握认为男生和女生的评分有差异?
附: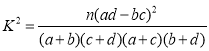 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |