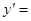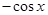题目内容
已知函数f(x)=ax-x3,对区间(0,1)上的任意x1,x2,且x1<x2,都有f(x2)-f(x1)>x2-x1成立,则实数a的取值范围为( )
| A.(0,1) | B.[4,+∞) | C.(0,4] | D.(1,4] |
B
问题等价于函数g(x)=f(x)-x在(0,1)上为增函数,即g′(x)=a-1-3x2≥0,即a≥1+3x2在(0,1)上恒成立,即a≥4,所以实数a的取值范围是[4,+∞).

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
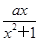 +a,g(x)=aln x-x(a≠0).
+a,g(x)=aln x-x(a≠0).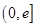 ,总有g(x1)<f(x2)成立.
,总有g(x1)<f(x2)成立.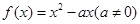 ,
,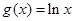 ,
,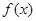 图象与
图象与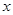 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为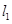 ,
,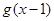 与
与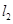 , 并且
, 并且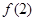 的值;
的值;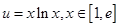 的取值范围及函数
的取值范围及函数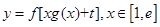 的最小值;
的最小值;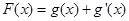 ,给定
,给定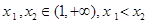 ,对于两个大于1的正数
,对于两个大于1的正数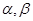 ,存在实数
,存在实数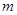 满足:
满足: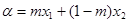 ,
,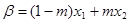 ,并且使得不等式
,并且使得不等式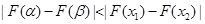 恒成立,求实数
恒成立,求实数
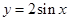 的导数
的导数