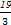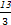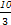题目内容
设命题P:函数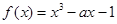 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;
命题q:函数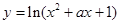 的定义域为R.若命题p或q为假命题,求
的定义域为R.若命题p或q为假命题,求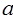 的取值范围.
的取值范围.
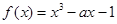 在区间[-1,1]上单调递减;
在区间[-1,1]上单调递减;命题q:函数
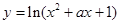 的定义域为R.若命题p或q为假命题,求
的定义域为R.若命题p或q为假命题,求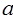 的取值范围.
的取值范围.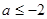 或
或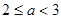
试题分析:利用导数求出命题
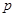 为真时
为真时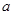 的取值集合
的取值集合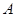 ,利用二次函 数的知识求出命题
,利用二次函 数的知识求出命题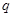 为真时
为真时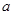 的取值集合
的取值集合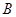 ,由命题p或q为假命题知,命题
,由命题p或q为假命题知,命题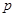 、
、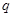 均为假命题,所以
均为假命题,所以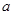 的取值集合为
的取值集合为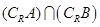
试题解析:解:因为
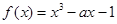
所以
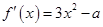
函数
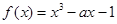 在区间[-1,1]上单调递减
在区间[-1,1]上单调递减所以
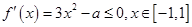
即
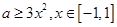
因为当
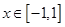 时,
时,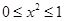 ,
,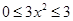
所以
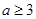 ,
,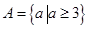
因为函数
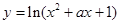 的定义域为R
的定义域为R所以,
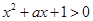 在
在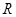 上恒成立
上恒成立所以有,
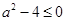 ,解得:
,解得: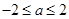 ,即
,即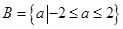
由于命题p或q为假命题,所以命题
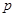 、
、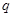 均为假命题,
均为假命题,所以
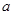 的取值集合为
的取值集合为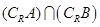 =
=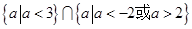
=
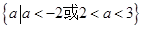

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 ,
,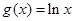 ,
,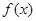 图象与
图象与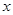 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为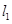 ,
,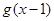 与
与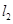 , 并且
, 并且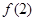 的值;
的值;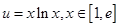 的取值范围及函数
的取值范围及函数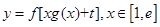 的最小值;
的最小值;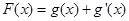 ,给定
,给定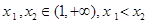 ,对于两个大于1的正数
,对于两个大于1的正数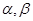 ,存在实数
,存在实数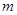 满足:
满足: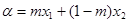 ,
,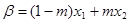 ,并且使得不等式
,并且使得不等式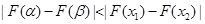 恒成立,求实数
恒成立,求实数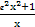 ,g(x)=
,g(x)=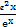 ,对任意x1,x2∈(0,+∞),不等式
,对任意x1,x2∈(0,+∞),不等式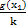 ≤
≤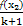 恒成立,则正数k的取值范围是 .
恒成立,则正数k的取值范围是 .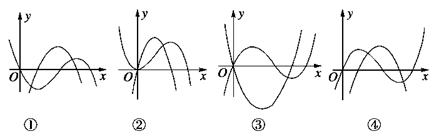
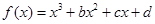 (
(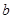 、
、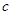 、
、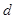 为常数),当
为常数),当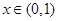 时取极大值,当
时取极大值,当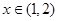 时取极小值,则
时取极小值,则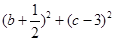 的取值范围是( )
的取值范围是( )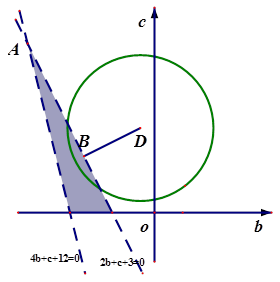
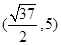
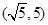
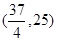
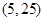
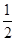 mx2+ln x-2x在定义域内是增函数,则实数m的取值范围是________.
mx2+ln x-2x在定义域内是增函数,则实数m的取值范围是________.