题目内容
12.△ABC的内角A、B、C所对边的长为a、b、c,且2bsinA=a,若△ABC为锐角三角形,则角B的大小为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 根据正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由△ABC为锐角三角形可得答案.
解答 解:由a=2bsinA,
根据正弦定理得sinA=2sinBsinA,所以sinB=$\frac{1}{2}$,
由△ABC为锐角三角形得B=$\frac{π}{6}$.
故选:B.
点评 本题主要考查正弦定理的应用.在解三角形中正余弦定理应用的很广泛,一定要熟练掌握公式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
7.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$的值的一个程序框图,则判断框内应填入的条件是( ) 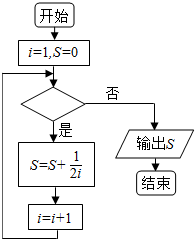

| A. | i≤1 005? | B. | i>1 005? | C. | i≤1 006? | D. | i>1 006? |
17.设x、y满足约束条件$\left\{\begin{array}{l}2x+y-6≥0\\ x+2y-6≤0\\ y≥0\end{array}\right.$,则目标函数z=2x+y的最大值是6.
1.已知△ABC中,AB=$\sqrt{3}$,AC=2,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则$\overrightarrow{AO}$•$\overrightarrow{BC}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
2.一个袋子中有号码为1,2,3,4大小相同的4个小球,现从中任意取出一个球,取出后再放回,然后再从
袋中任取一个球,则取得两个号码之和为5的概率为( )
袋中任取一个球,则取得两个号码之和为5的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{16}$ |