题目内容
1.已知△ABC中,AB=$\sqrt{3}$,AC=2,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则$\overrightarrow{AO}$•$\overrightarrow{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 由$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,可得点O为△ABC的重心,不妨取BC=1,则∠ABC=90°,如图所示.利用数量积的坐标运算性质即可得出.
解答 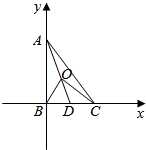 解:由$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,可得点O为△ABC的重心,
解:由$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,可得点O为△ABC的重心,
不妨取BC=1,则∠ABC=90°,如图所示.
则A$(0,\sqrt{3})$,C(1,0),D$(\frac{1}{2},0)$,O$(\frac{1}{3},\frac{\sqrt{3}}{3})$,
$\overrightarrow{AO}$=$(\frac{1}{3},-\frac{2\sqrt{3}}{3})$,$\overrightarrow{BC}$=(1,0),
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{3}$.
故选:C.
点评 本题考查了数量积的坐标运算性质、三角形的重心性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
18.某市举行“希望杯”足球比赛,由全市的6支企业职工业余足球队参加,比赛组委会规定:比赛实行单循环制,每个队胜一场得3分,平一场得1分,负一场得0分,在今年即将举行的“希望杯”足球比赛中,参加比赛的市工商银行对可能的积分值有( )
| A. | 13种 | B. | 14种 | C. | 15种 | D. | 16种 |
12.△ABC的内角A、B、C所对边的长为a、b、c,且2bsinA=a,若△ABC为锐角三角形,则角B的大小为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
16.已知A={x|log3x>1},B={x|y=$\sqrt{x-1}$+$\sqrt{3-x}$},那么有( )
| A. | A∩B=∅ | B. | A⊆B | C. | B⊆A | D. | A=B |
13.若函数f(x)=$\sqrt{3}$sin2x-cos2x,则将f(x)向右平移$\frac{π}{3}$个单位所得曲线的一条对称轴方程为( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{2}$ | D. | x=π |
11.已知集合A={x|y=$\sqrt{x}$},且B⊆A,则集合B可能是( )
| A. | {1,2,3} | B. | {x|-1<x<1} | C. | {-2,2} | D. | R |
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).