题目内容
10.已知f(x)=x2-2ax+a-2.(a∈R).(1)当a=-1时,求不等式f(x)<0的解集;
(2)解关于x的不等式f(x)>f(a)
分析 (1)由题意可得x2+2x-3<0,即有(x-1)(x+3)<0,即可得到所求不等式的解集;
(2)代入化简整理,可得x2-2ax+a2>0,即为(x-a)2>0,即可求得解集.
解答 解:(1)当a=-1时,f(x)<0即为:
x2+2x-3<0,即有(x-1)(x+3)<0,
解得-3<x<1,则解集为(-3,1);
(2)f(x)>f(a)即为x2-2ax+a-2>-a2+a-2,
即x2-2ax+a2>0,即为(x-a)2>0,
解得x≠a,x∈R,
则解集为{x|x∈R,且x≠a}.
点评 本题考查二次不等式的解法,以及含参不等式的解法,注意运用分解因式,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.某市举行“希望杯”足球比赛,由全市的6支企业职工业余足球队参加,比赛组委会规定:比赛实行单循环制,每个队胜一场得3分,平一场得1分,负一场得0分,在今年即将举行的“希望杯”足球比赛中,参加比赛的市工商银行对可能的积分值有( )
| A. | 13种 | B. | 14种 | C. | 15种 | D. | 16种 |
12.△ABC的内角A、B、C所对边的长为a、b、c,且2bsinA=a,若△ABC为锐角三角形,则角B的大小为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
13.若函数f(x)=$\sqrt{3}$sin2x-cos2x,则将f(x)向右平移$\frac{π}{3}$个单位所得曲线的一条对称轴方程为( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{2}$ | D. | x=π |
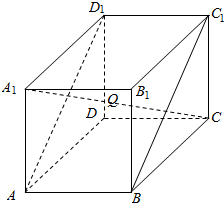 图所示的正方体ABCD-A1B1C1D1中,记直线A1C与平面ABC1D1交于点Q,求证:点B,Q,D1共线.
图所示的正方体ABCD-A1B1C1D1中,记直线A1C与平面ABC1D1交于点Q,求证:点B,Q,D1共线.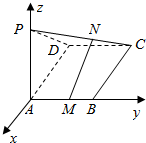 已知PA垂直于正方形ABCD所在的平面,M,N分别在AB,PC上,且PN=2NC,AM=2MB,PA=AD=1,如图建立空间直角坐标系,求$\overrightarrow{MN}$的坐标.
已知PA垂直于正方形ABCD所在的平面,M,N分别在AB,PC上,且PN=2NC,AM=2MB,PA=AD=1,如图建立空间直角坐标系,求$\overrightarrow{MN}$的坐标.