题目内容
(本题满分14分)数列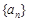 是公比为
是公比为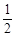 的等比数列,且
的等比数列,且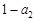 是
是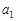 与
与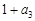 的等比中项,前
的等比中项,前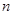 项和为
项和为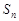 .数列
.数列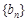 是等差数列,
是等差数列,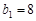 ,前
,前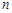 项和
项和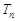 满足
满足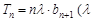 为常数,且
为常数,且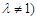 .
.
(Ⅰ)求数列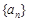 的通项公式及
的通项公式及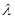 的值;
的值;
(Ⅱ)比较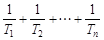 与
与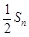 的大小.
的大小.
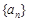 是公比为
是公比为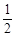 的等比数列,且
的等比数列,且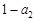 是
是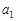 与
与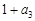 的等比中项,前
的等比中项,前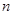 项和为
项和为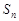 .数列
.数列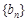 是等差数列,
是等差数列,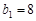 ,前
,前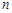 项和
项和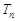 满足
满足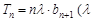 为常数,且
为常数,且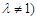 .
.(Ⅰ)求数列
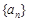 的通项公式及
的通项公式及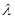 的值;
的值;(Ⅱ)比较
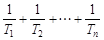 与
与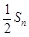 的大小.
的大小.(Ⅰ)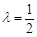 ;(Ⅱ)
;(Ⅱ)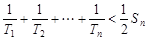 。
。
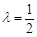 ;(Ⅱ)
;(Ⅱ)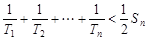 。
。本试题主要是考查了等差数列和等比数列,数列求和的综合运用。
(1)因为根据已知条件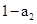 是
是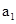 与
与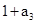 的等比中项,这样利用首项和公差得到其通项公式。和参数
的等比中项,这样利用首项和公差得到其通项公式。和参数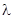 的值。
的值。
(2)由上知道,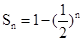 ,然后利用放缩法得到证明,同时利用
,然后利用放缩法得到证明,同时利用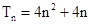 ,裂项求和得到结论。
,裂项求和得到结论。
解(Ⅰ)由题意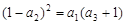 ,即
,即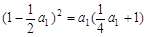 (2分)
(2分)
解得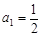 ,∴
,∴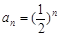 (4分)
(4分)
又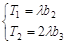 ,即
,即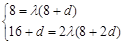 (6分)
(6分)
解得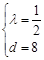 或
或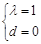 (舍)∴
(舍)∴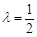 (8分)
(8分)
(Ⅱ)由(Ⅰ)知
∴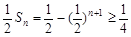 ①(10分)
①(10分)
又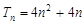 ,
,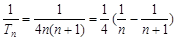
∴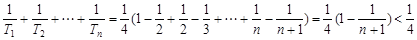 ②(13分)
②(13分)
由①②可知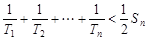 (14分)
(14分)
(1)因为根据已知条件
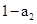 是
是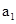 与
与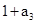 的等比中项,这样利用首项和公差得到其通项公式。和参数
的等比中项,这样利用首项和公差得到其通项公式。和参数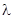 的值。
的值。(2)由上知道,
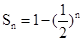 ,然后利用放缩法得到证明,同时利用
,然后利用放缩法得到证明,同时利用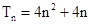 ,裂项求和得到结论。
,裂项求和得到结论。解(Ⅰ)由题意
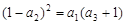 ,即
,即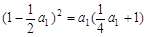 (2分)
(2分)解得
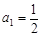 ,∴
,∴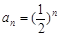 (4分)
(4分)又
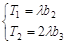 ,即
,即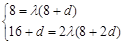 (6分)
(6分)解得
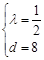 或
或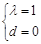 (舍)∴
(舍)∴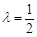 (8分)
(8分)(Ⅱ)由(Ⅰ)知

∴
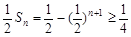 ①(10分)
①(10分)又
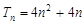 ,
,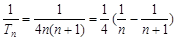
∴
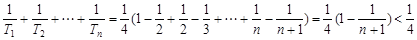 ②(13分)
②(13分)由①②可知
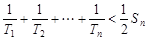 (14分)
(14分)
练习册系列答案
相关题目
 ,数列
,数列 满足
满足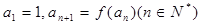 .
.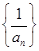 是等差数列,并求数列
是等差数列,并求数列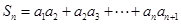 ,求
,求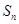 .
.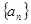 的前
的前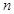 项和为
项和为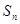 ,已知
,已知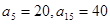 ,
,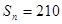 ,求
,求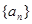 是公差为正数的等差数列,若
是公差为正数的等差数列,若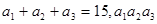 =80,则
=80,则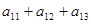 =
=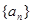 为等差数列,公差为
为等差数列,公差为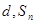 为其前
为其前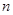 项和,
项和,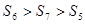 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )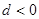
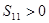
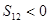
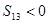
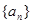 满足
满足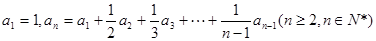 .若
.若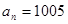 ,则
,则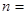 _____________.
_____________.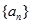 的首项
的首项 及公差
及公差 都是整数,前
都是整数,前 项和为
项和为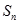 ,若
,若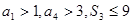 ,设
,设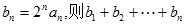 的结果为 。
的结果为 。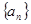 是等差数列,
是等差数列,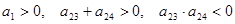 ,则使前
,则使前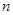 项和
项和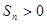 成立的最大正数
成立的最大正数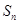 是等差数列
是等差数列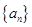 的前
的前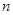 项和,已知
项和,已知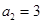 ,
,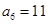 ,则
,则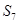 等于( )
等于( )