题目内容
【题目】已知a1=2，点（an ， an+1）在函数f（x）=x2+2x的图象上，其中n=1，2，3，…．
（1）求a3 ， a4的值；
（2）证明数列{lg（1+an）}是等比数列，并求数列{an}的通项公式；
（3）记bn= 
+ 
，求数列{bn}的前n项和Sn ．
【答案】
（1）解：∵a1=2，点（an，an+1）在函数f（x）=x2+2x的图象上，其中n=1，2，3，…．
∴ 
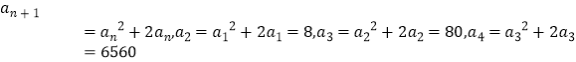
（2）证明：∵ 
，
∴{lg（1+an）}是首项为lg3，公比为2的等比数列，
∴ 
（3）解： 
，
∴ 
，
∴ 
【解析】（1）由已知得a1=2，an+1=an2+2an ， 由此利用递推思想能求出a3 ， a4的值．（2）由 ，能数列{lg（1+an）}是等比数列，并能求出数列{an}的通项公式．（3）推导出 ，由此利用裂项求和法能求出数列{bn}的前n项和Sn ．
【考点精析】本题主要考查了等比数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：
；数列{an}的前n项和sn与通项an的关系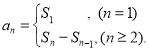
才能正确解答此题．
名师点拨卷系列答案【题目】我省城乡居民社会养老保险个人年缴费分100，200，300，400，500，600，700，800，900，1000（单位：元）十个档次，某社区随机抽取了50名村民，按缴费在100：500元，600：1000元，以及年龄在20：39岁，40：59岁之间进行了统计，相关数据如下：
100﹣500元 | 600﹣1000 | 总计 | |
20﹣39 | 10 | 6 | 16 |
40﹣59 | 15 | 19 | 34 |
总计 | 25 | 25 | 50 |
（1）用分层抽样的方法在缴费100：500元之间的村民中随机抽取5人，则年龄在20：39岁之间应抽取几人？
（2）在缴费100：500元之间抽取的5人中，随机选取2人进行到户走访，求这2人的年龄都在40：59岁之间的概率．
