题目内容
【题目】已知函数f(x)=![]() -x2+ef′(
-x2+ef′(![]() )x.
)x.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在x1,x2(x1<x2),使得f(x1)+f(x2)=1,求证:x1+x2<2.
【答案】(Ⅰ)在R上单调递增;(Ⅱ)见解析
【解析】
(I)f′(x)=e2(x-1)-2x+ef′(![]() ).令x=
).令x=![]() ,则f′(
,则f′(![]() )=
)=![]() -1+ef′(
-1+ef′(![]() ),解得f′(
),解得f′(![]() ),进而得出函数f(x)的单调性.
),进而得出函数f(x)的单调性.
(II)由(I)可得:函数f(x))=![]() -x2+x在R上单调递增.要证明:x1+x2<2x1<2-x2f(x1)<f(2-x2),又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),即f(x2)+f(2-x2)-1>0,f(1)=
-x2+x在R上单调递增.要证明:x1+x2<2x1<2-x2f(x1)<f(2-x2),又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),即f(x2)+f(2-x2)-1>0,f(1)=![]() -1+1=
-1+1=![]() ,则x1<1<x2.令g(x)=f(2-x)+f(x)-1=
,则x1<1<x2.令g(x)=f(2-x)+f(x)-1=![]() +
+![]() -2x2+4x-2,x>1,g(1)=0.利用导数研究其单调性即可证明结论.
-2x2+4x-2,x>1,g(1)=0.利用导数研究其单调性即可证明结论.
(I)f′(x)=e2(x-1)-2x+ef′(![]() ).
).
令x=![]() ,则f′(
,则f′(![]() )=
)=![]() -1+ef′(
-1+ef′(![]() ),解得f′(
),解得f′(![]() )=
)=![]() .
.
∴f′(x)=e2(x-1)-2x+1.f″(x)=2e2(x-1)-2=2(ex-1+1)(ex-1-1),
![]() 时
时![]() 单调递增;
单调递增;![]() 时
时![]() 单调递减,
单调递减,
∴x=1时,函数f′(x)取得极小值即最小值,∴f′(x)≥f′(1)=0,
∴函数f(x)在R上单调递增.
(II)由(I)可得:函数f(x)=![]() -x2+x在R上单调递增.
-x2+x在R上单调递增.
要证明:x1+x2<2x1<2-x2f(x1)<f(2-x2),
又f(x1)+f(x2)=1,因此f(x1)<f(2-x2)1-f(x2)<f(2-x2),
即f(x2)+f(2-x2)-1>0,f(1)=![]() =
=![]() ,则x1<1<x2.
,则x1<1<x2.
令g(x)=f(2-x)+f(x)-1=![]() -(2-x)2+2-x+
-(2-x)2+2-x+![]() -x2+x=
-x2+x=![]() +
+![]() -2x2+4x-2,x>1,g(1)=0.g′(x)=-e2(1-x)+e2(x-1)-4x+4,
-2x2+4x-2,x>1,g(1)=0.g′(x)=-e2(1-x)+e2(x-1)-4x+4,
g″(x)=2e2(1-x)+2e2(x-1)-4≥0,∴g′(x)在(1,+∞)上单调递增.
∴g′(x)>g′(1)=0,∴函数g(x)在(1,+∞)上单调递增.
∴g(x)>g(1)=0,因此结论x1+x2<2成立.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有![]() 选择了退货.
选择了退货.
(1)请完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“客户购买产品与对产品性能满意之间有关”.
的把握认为“客户购买产品与对产品性能满意之间有关”.
对性能满意 | 对性能不满意 | 合计 | |
购买产品 | |||
不购买产品 | |||
合计 |
(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有4张奖券,奖券上分别印有200元、400元、600元和800元字样,抽到奖券可获得相应奖金.6位客户有放回的进行抽取,每人随机抽取一张奖券,求6位客户中购买产品的客户人均所得奖金不少于500元的概率.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】画糖人是一种以糖为材料在石板上进行造型的民间艺术.某糖人师傅在公园内画糖人,每天卖出某种糖人的个数与价格相关,其相关数据统计如下表:
每个糖人的价格 | 9 | 10 | 11 | 12 | 13 |
卖出糖人的个数 | 54 | 50 | 46 | 43 | 39 |
(1)根据表中数据求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若该种造型的糖人的成本为2元/个,为使糖人师傅每天获得最大利润,则该种糖人应定价多少元?(精确到1元)
参考公式:回归直线方程![]() ,其中
,其中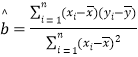 ,
,![]() .
.