题目内容
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(3,m)在抛物线E上,且|AF|=4. 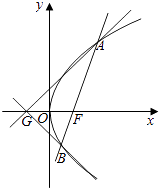
(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
【答案】
(1)解:由抛物线定义可得:|AF|=3+ ![]() =4,解得p=2.
=4,解得p=2.
∴抛物线E的方程为y2=4x;
(2)证明:∵点A(3,m)在抛物线E上,
∴m2=4×3,解得m=±2 ![]() ,不妨取A(3,2
,不妨取A(3,2 ![]() ),F(1,0),
),F(1,0),
∴直线AF的方程:y= ![]() (x﹣1),
(x﹣1),
联立抛物线,化为3x2﹣10x+3=0,解得x=3或 ![]() ,B(
,B( ![]() ,﹣
,﹣ ![]() ).
).
又G(﹣1,0),∴kGA= ![]() .kGB=﹣
.kGB=﹣ ![]() ,
,
∴kGA+kGB=0,
∴∠AGF=∠BGF,∴x轴平分∠AGB,
因此点F到直线GA,GB的距离相等,
∴以点F为圆心且与直线GA相切的圆,必与直线GB相切.
【解析】(1)由抛物线定义可得:|AF|=3+ ![]() =4,解得p.即可得出抛物线E的方程.(2)由点A(3,m)在抛物线E上,解得m,不妨取A(3,2
=4,解得p.即可得出抛物线E的方程.(2)由点A(3,m)在抛物线E上,解得m,不妨取A(3,2 ![]() ),F(1,0),可得直线AF的方程,与抛物线方程联立化为3x2﹣10x+3=0,解得B(
),F(1,0),可得直线AF的方程,与抛物线方程联立化为3x2﹣10x+3=0,解得B( ![]() ,﹣
,﹣ ![]() ).又G(﹣1,0),计算kGA , kGB , 可得kGA+kGB=0,∠AGF=∠BGF,即可证明以点F为圆心且与直线GA相切的圆,必与直线GB相切.
).又G(﹣1,0),计算kGA , kGB , 可得kGA+kGB=0,∠AGF=∠BGF,即可证明以点F为圆心且与直线GA相切的圆,必与直线GB相切.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目