题目内容
求经过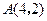 ,
,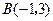 两点,且在两坐标轴上的四个截距之和为
两点,且在两坐标轴上的四个截距之和为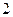 的圆的方程.
的圆的方程.
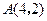 ,
,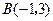 两点,且在两坐标轴上的四个截距之和为
两点,且在两坐标轴上的四个截距之和为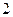 的圆的方程.
的圆的方程.所求圆的方程为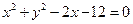
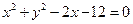
设所求圆的方程为 ①
①
 圆经过
圆经过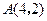 ,
,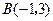 两点,则有
两点,则有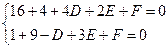
即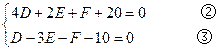
令①中的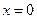 ,得
,得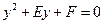 ,由韦达定理
,由韦达定理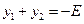 .
.
令①中的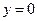 ,得
,得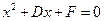 ,
,
由韦达定理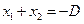 .
.
由于所求圆在两坐标轴上的四个截距之和为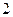 ,从而有
,从而有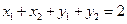 ,
,
即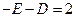 ,也就是
,也就是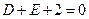 ④
④
由②③④可得到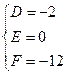
 所求圆的方程为
所求圆的方程为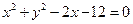 .
.
 ①
① 圆经过
圆经过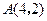 ,
,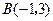 两点,则有
两点,则有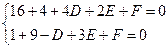
即
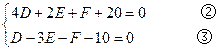
令①中的
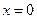 ,得
,得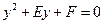 ,由韦达定理
,由韦达定理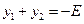 .
.令①中的
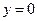 ,得
,得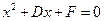 ,
,由韦达定理
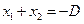 .
.由于所求圆在两坐标轴上的四个截距之和为
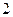 ,从而有
,从而有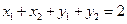 ,
,即
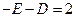 ,也就是
,也就是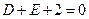 ④
④由②③④可得到
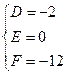
 所求圆的方程为
所求圆的方程为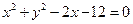 .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,
, 相切,圆心在直线
相切,圆心在直线 上,求这个圆的方程.
上,求这个圆的方程. ,若该方程表示一个圆,求
,若该方程表示一个圆,求 的取值范围及这时圆心的轨迹方程.
的取值范围及这时圆心的轨迹方程. 的圆心在
的圆心在 轴上,并且过点
轴上,并且过点 和
和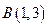 ,求圆
,求圆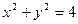 上运动,线段PQ的中点为M,求点M的轨迹方程
上运动,线段PQ的中点为M,求点M的轨迹方程 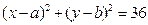 的曲线经过点
的曲线经过点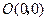 和点
和点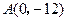 ,求
,求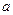 ,
,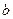 的值.
的值.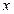 轴相切,半径为
轴相切,半径为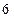 ,圆心的横坐标为
,圆心的横坐标为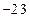 的圆的方程为( ).
的圆的方程为( ).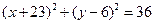
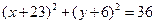

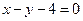 上,并且过圆
上,并且过圆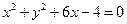 与圆
与圆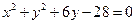 的交点的圆的方程.
的交点的圆的方程.