题目内容
【题目】某消费品专卖店的经营资料显示如下:
①这种消费品的进价为每件14元;
②该店月销售量Q(百件)与销售价格P(元)满足的函数关系式为Q= ![]() ,点(14,22),(20,10),(26,1)在函数的图象上;
,点(14,22),(20,10),(26,1)在函数的图象上;
③每月需各种开支4400元.
(1)求月销量Q(百件)与销售价格P(元)的函数关系;
(2)当商品的价格为每件多少元时,月利润最大?并求出最大值.
【答案】
(1)解:∵点(14,22),(20,10),(26,1)在函数的图象上,
∴ ![]() ,解得
,解得 ![]() .
.
同理可得 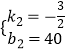 ,
,
∴Q= 
(2)解:设该店月利润为L元,则由题设得L=Q(P﹣14)×100﹣100,
由(1)得L= 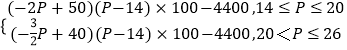 ,
,
= ![]() ,
,
当14≤p≤20时,Lmax=1650元,此时P= ![]() 元,
元,
当20<p≤26时,Lmax= ![]() 元,此时P=
元,此时P= ![]() 元,
元,
故当P= ![]() 时,月利润最大,为1650元
时,月利润最大,为1650元
【解析】(1)利用带待定系数法即可求出函数的解析式,再根据销售量Q(百件)与销售价格P(元)满足的函数关系式,即可月销量Q(百件)与销售价格P(元)的函数关系,(2)设该店月利润为L元,则由题设得L=Q(P﹣14)×100﹣100,得到函数的解析式,分段求出函数的最值,比较即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目