Question

【题目】已知函数f（x）=x2﹣4x+3，g（x）=m（x﹣1）+2（m＞0），若存在x1∈[0，3]，使得对任意的x2∈[0，3]，都有f（x1）=g（x2），则实数m的取值范围是（ ）
A.
B.（0，3]
C.
D.[3，+∞）

Answer 1

【答案】A
【解析】解：存在x1∈[0，3]，使得对任意的x2∈[0，3]，都有f（x1）=g（x2） {g（x）|x∈[0，3]}{f（x）|x∈[0，3]}．
∵函数f（x）=x2﹣4x+3=（x﹣2）2﹣1，x∈[0，3]．
∴当x=2时，函数f（x）取得最小值f（2）=﹣1．又f（0）=3，f（3）=0．
∴函数f（x）的值域为[﹣1，3]．
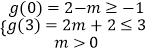∴ ，解得0＜m≤ ．
故选：A．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．