题目内容
设函数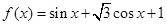 ,
,
(I)求函数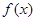 在
在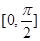 上的最大值与最小值;
上的最大值与最小值;
(II)若实数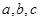 使得
使得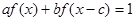 对任意
对任意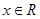 恒成立,求
恒成立,求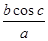 的值.
的值.
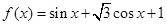 ,
,(I)求函数
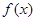 在
在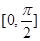 上的最大值与最小值;
上的最大值与最小值;(II)若实数
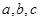 使得
使得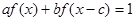 对任意
对任意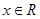 恒成立,求
恒成立,求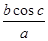 的值.
的值.(I)最大值为3,最小值为2(II)-1
试题分析:(I)将函数
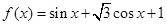 化为
化为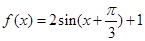 ,再求出最值;
,再求出最值;(II)由
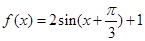 和
和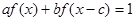 求出a、b、c,再将值代入
求出a、b、c,再将值代入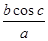 。
。解:(I)由条件知
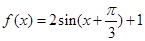 ,
,由
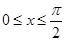 知,
知,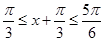 ,于是
,于是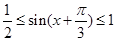
所以
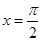 时,
时,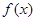 有最小值
有最小值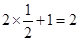 ;
;当
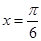 时,
时,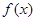 有最大值
有最大值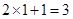 .
.(II)由条件可知
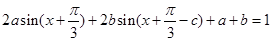 对任意的
对任意的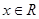 恒成立,
恒成立,∴
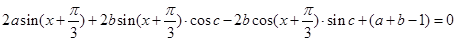
∴
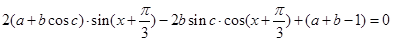
∴
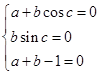 ,
,由
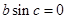 知
知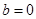 或
或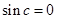 .
.若
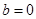 时,则由
时,则由 知
知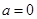 ,这与
,这与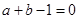 矛盾!
矛盾!若
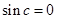 ,则
,则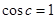 (舍去),
(舍去),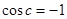 ,
,解得
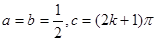 ,所以,
,所以,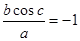
点评:本题主要考查两角和与差的正弦公式和正弦函数的性质:单调性、最值.考查考生对基础知识的掌握程度和熟练应用程度.

练习册系列答案
相关题目
 ,
,  .
. 的最大值和最小值;
的最大值和最小值; 上的图象与
上的图象与 轴的交点从左到右分别为
轴的交点从左到右分别为 ,图象的最高点为
,图象的最高点为 ,
, 与
与 的夹角的余弦.
的夹角的余弦.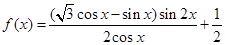 .
.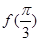 的值;
的值;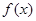 的最小正周期及单调递减区间.
的最小正周期及单调递减区间. 中的内角
中的内角 、
、 、
、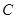 的对边分别为
的对边分别为 、
、 、
、 ,定义向量
,定义向量 ,
, ,且
,且 .
. 的单调减区间;
的单调减区间; ,求
,求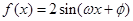 的图像如图所示,则
的图像如图所示,则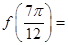 。
。
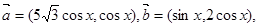 设函数
设函数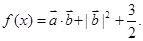 (Ⅰ)当
(Ⅰ)当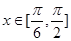 ,求函数
,求函数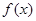 的值域;
的值域;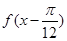 的值;
的值; ,则
,则




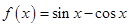 ,则
,则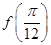 的值是( )
的值是( )


