题目内容
已知函数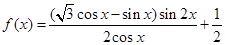 .
.
(Ⅰ)求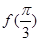 的值;
的值;
(Ⅱ)求函数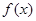 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.
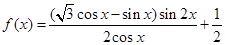 .
.(Ⅰ)求
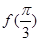 的值;
的值;(Ⅱ)求函数
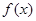 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.(Ⅰ) ;(Ⅱ)最小正周期为
;(Ⅱ)最小正周期为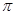 ,单调递减区间为
,单调递减区间为 .
.
 ;(Ⅱ)最小正周期为
;(Ⅱ)最小正周期为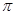 ,单调递减区间为
,单调递减区间为 .
.试题分析:(1)直接计算
 的值,若式子的结果较复杂时,一般将函数解析式先化简再求值;(2)求函数
的值,若式子的结果较复杂时,一般将函数解析式先化简再求值;(2)求函数 的最小正周期、单调区间等基本性质,一般先将函数解析式进行化简,即一般将三角函数解析式化为
的最小正周期、单调区间等基本性质,一般先将函数解析式进行化简,即一般将三角函数解析式化为 的形式,然后利用公式
的形式,然后利用公式 即可求出函数
即可求出函数 的最小正周期,利用复合函数法结合正弦函数的单调性即可求出函数
的最小正周期,利用复合函数法结合正弦函数的单调性即可求出函数 相应的单调区间,但首先应该求函数的定义域.
相应的单调区间,但首先应该求函数的定义域.试题解析:解(Ⅰ)



 4分
4分(Ⅱ)由

故
 的定义域为
的定义域为
因为






所以
 的最小正周期为
的最小正周期为
因为函数
 的单调递减区间为
的单调递减区间为 ,
,由

得

所以
 的单调递减区间为
的单调递减区间为
13分

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
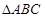 中,角
中,角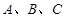 所对的边分别为
所对的边分别为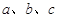 ,已知
,已知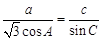 ,
,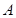 的大小;
的大小;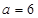 ,求
,求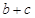 的取值范围.
的取值范围. ,
, .
. 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
,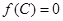 且
且 ,求
,求 的始边与
的始边与 轴的非负半轴重合,终边过点
轴的非负半轴重合,终边过点 ,则
,则



 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( ) 的图象关于直线
的图象关于直线 对称
对称
 上是增函数
上是增函数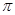
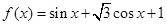 ,
,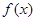 在
在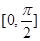 上的最大值与最小值;
上的最大值与最小值;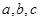 使得
使得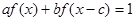 对任意
对任意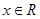 恒成立,求
恒成立,求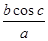 的值.
的值.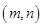 ,
,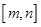 ,
,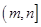 ,
,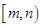 的长度均为
的长度均为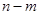 ,其中
,其中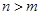 .
.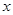 的不等式
的不等式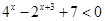 的解集构成的区间的长度;
的解集构成的区间的长度;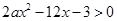 的解集构成的区间的长度为
的解集构成的区间的长度为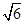 ,求实数
,求实数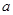 的值;
的值;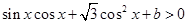 ,
,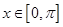 的解集构成的各区间的长度和超过
的解集构成的各区间的长度和超过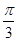 ,求实数
,求实数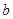 的取值范围.
的取值范围.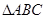 中,角
中,角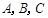 所对的边分别为
所对的边分别为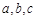 ,且满足
,且满足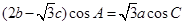 .
. 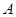 的大小;
的大小; 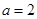 ;②
;②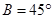 ;③
;③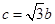 .试从中选出两个可以确定
.试从中选出两个可以确定 ,则
,则 ( )
( )


