题目内容
设偶函数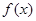 的定义域为R,当
的定义域为R,当 时,
时, 是增函数,则
是增函数,则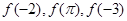 的大小关系是( )
的大小关系是( )
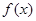 的定义域为R,当
的定义域为R,当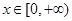 时,
时,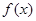 是增函数,则
是增函数,则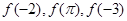 的大小关系是( )
的大小关系是( )A.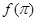 > >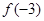 > >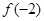 | B.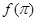 > >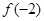 > >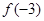 |
C.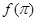 < <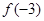 < <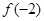 | D.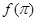 < <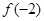 < <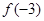 |
A
试题分析:由偶函数的性质,知若x∈[0,+∞)时f(x)是增函数则x∈(-∞,0)时,
f(x)是减函数,此函数的几何特征是自变量的绝对值越小,则其函数值越小,故比较三式大小的问题,转化成比较三式中自变量-2,-3,π的绝对值大小的问题。
解:由偶函数与单调性的关系知,若x∈[0,+∞)时f(x)是增函数则x∈(-∞,0)时f(x)是减函数,故其图象的几何特征是自变量的绝对值越小,则其函数值越小,∵|-2|<|-3|<π,∴f(π)>f(-3)>f(-2),故选A.
点评:本题考点是奇偶性与单调性的综合,对于偶函数,在对称的区间上其单调性相反,且自变量相反时函数值相同,将问题转化为比较自变量的绝对值的大小,做题时要注意此题转化的技巧

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
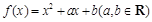 ,
,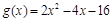 ,且
,且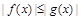 对
对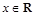 恒成立.
恒成立.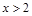 ,不等式
,不等式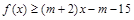 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.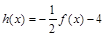 ,那么当
,那么当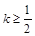 时,是否存在区间
时,是否存在区间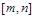 (
(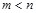 ),使得函数
),使得函数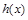 在区间
在区间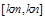 ?若存在,请求出区间
?若存在,请求出区间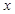
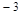
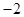
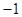
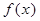
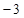


 ( )
( )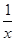 -2(x<0),则f(x)的最大值为
-2(x<0),则f(x)的最大值为 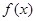 是定义在
是定义在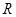 上的偶函数,当
上的偶函数,当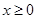 时,
时,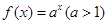 .
.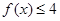 的解集为
的解集为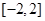 ,求
,求 的值.
的值.
 的单调区间和值域。
的单调区间和值域。 ,求函数
,求函数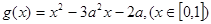 ,若对于任意
,若对于任意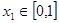 ,总存在
,总存在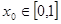 ,使得
,使得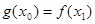 成立,求实数
成立,求实数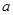 的取值范围。
的取值范围。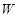 与它的航行速度
与它的航行速度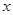 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;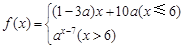 若数列{an}满足an=
若数列{an}满足an=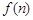 (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )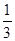 ,1)
,1)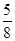 )
)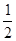 )
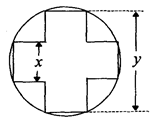
)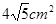 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽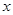 及长
及长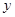 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.