题目内容
已知f(x)=x+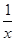 -2(x<0),则f(x)的最大值为
-2(x<0),则f(x)的最大值为
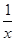 -2(x<0),则f(x)的最大值为
-2(x<0),则f(x)的最大值为 -4
试题分析:根据已知条件可知,f(x)=x+
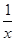 -2(x<0),那么可知结合均值不等式,有
-2(x<0),那么可知结合均值不等式,有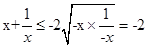 解可知f(x)=x+
解可知f(x)=x+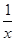 -2
-2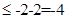 ,当且仅当
,当且仅当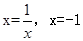 时取得等号,故可知答案为-4.
时取得等号,故可知答案为-4.点评:主要是考查了均值不等式求解函数的最值,注意运用一正二定三相等来准确的求解和运算,属于基础题。

练习册系列答案
相关题目
题目内容
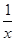 -2(x<0),则f(x)的最大值为
-2(x<0),则f(x)的最大值为 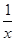 -2(x<0),那么可知结合均值不等式,有
-2(x<0),那么可知结合均值不等式,有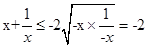 解可知f(x)=x+
解可知f(x)=x+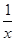 -2
-2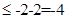 ,当且仅当
,当且仅当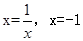 时取得等号,故可知答案为-4.
时取得等号,故可知答案为-4.