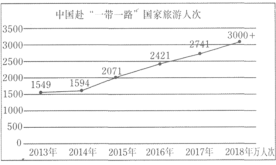
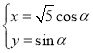题目内容
【题目】由0123456可以组成多少个没有重复数字的
(1)五位数;
(2)五位偶数;
(3)能被5整除的五位数.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
(1)首先在除0外的剩余数中选择一个安排在万位,然后剩余6个数进行全排列;(2)分末位为0与末位不为0两种情况计算可以组成的无重复数字的五位偶数,求和即可;(3)分末位为0与末位为5两种情况求出能组成的被5整除的五位数的个数,求和即可.
(1)首先在除0外的剩余数中选择一个安排在首位,
然后从剩余6个数中选择4个数进行全排列,
共有![]() 种排列方式;
种排列方式;
(2)由0123456可以组成![]() 个末位为0的五位偶数,
个末位为0的五位偶数,
![]() 个末位不为0的五位偶数,
个末位不为0的五位偶数,
所以共可以组成2140个没有重复数字的五位偶数;
(3)末位为0,则前4位从剩余6个数中抽取4个进行全排列,
共能排出![]() 种能被5整除的五位数;
种能被5整除的五位数;
末位为5,首先从1、2、3、4、6中选1个数排在首位,
然后从剩余的5个数中抽取3个数排列在中间三位,
可以组成![]() 个能被5整除的五位数,
个能被5整除的五位数,
所以共可以组成![]() 个能被5整除的五位数.
个能被5整除的五位数.

练习册系列答案
相关题目
【题目】某工厂为了对本工厂工人的理论成绩与实践能力进行分析,决定从本工厂工人中随机抽取一个样本容量为7的样本进行分析.如果随机抽取的7名工人的理论成绩与实践能力值![]() 单位:分
单位:分![]() 对应如下表:
对应如下表:
工人序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
理论成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
实践能力值 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
(1)求这7名工人的理论成绩![]() 与实践能力值
与实践能力值![]() 的中位数、极差;
的中位数、极差;
(2)若规定85分以上![]() 包括85分
包括85分![]() 为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
为优秀,从这7名工人中抽取3名工人,记3名工人中理论成绩和实践能力值均为优秀的人数为X,求X的分布列和期望;
(3)根据下表数据,求实践能力值y关于理论成绩x的线性回归方程.![]() 系数精确到
系数精确到![]()
附:线性回归方程![]() 中,
中,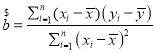 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |