题目内容
给定椭圆C：
+
=1(a＞b＞0)，称圆心在原点O、半径是
的圆为椭圆C的“准圆”．已知椭圆C的一个焦点为F(
，0)，其短轴的一个端点到点F的距离为
．
（1）求椭圆C和其“准圆”的方程；
（2）若点A是椭圆C的“准圆”与x轴正半轴的交点，B，D是椭圆C上的两相异点，且BD⊥x轴，求
•
的取值范围；
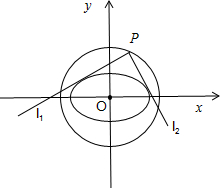
（3）在椭圆C的“准圆”上任取一点P，过点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，试判断l1，l2是否垂直？并说明理由．
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 3 |
（1）求椭圆C和其“准圆”的方程；
（2）若点A是椭圆C的“准圆”与x轴正半轴的交点，B，D是椭圆C上的两相异点，且BD⊥x轴，求
| AB |
| AD |
（3）在椭圆C的“准圆”上任取一点P，过点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，试判断l1，l2是否垂直？并说明理由．
（1）由题意可得：a=
，c=
，b=1，∴r=
=2．
∴椭圆C的方程为
+y2=1，其“准圆”的方程为x2+y2=4；
（2）由“准圆”的方程为x2+y2=4，令y=0，解得x=±2，取点A（2，0）．
设点B（x0，y0），则D（x0，-y0）．
∴
•
=（x0-2，y0）•（x0-2，-y0）=(x0-2)2-y02，
∵点B在椭圆
+y2=1上，∴
+y02=1，∴y02=1-
，
∴
•
=(x0-2)2-1+
=
(x0-
)2，
∵-
＜x0＜
，∴0≤
(x0-
)2＜7+4
，
∴0≤
•
＜7+4
，即
•
的取值范围为[0，7+4
)
（3）①当过准圆上点P的直线l与椭圆相切且其中一条直线的斜率为0而另一条斜率不存在时，则点P为(±
，±1)，此时l1⊥l2；
②当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，设点P（x0，y0），直线l的方程为m（y-y0）=x-x0．
联立
消去x得到关于y的一元二次方程：
(3+m2)y2+(2mx0-2m2y0)y+m2y02+x02-2mx0y0-3=0，
∴△=(2mx0-2m2y0)2-4(3+m2)(m2y02+x02-2mx0y0-3)=0，
化为(y02-1)m2-2mx0y0+x02-3=0，
∵y02-1≠0，m存在，∴m1m2=
．
∵点P在准圆上，∴x02+y02=4，∴x02-3=1-y02，
∴m1m2═-1．
即直线l1，l2的斜率kl1•kl2=-1，因此当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，直线l1⊥l2．
综上可知：在椭圆C的“准圆”上任取一点P，过点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，l1⊥l2．
| 3 |
| 2 |
(
|
∴椭圆C的方程为
| x2 |
| 3 |
（2）由“准圆”的方程为x2+y2=4，令y=0，解得x=±2，取点A（2，0）．
设点B（x0，y0），则D（x0，-y0）．
∴
| AB |
| AD |
∵点B在椭圆
| x2 |
| 3 |
| x02 |
| 3 |
| x02 |
| 3 |
∴
| AD |
| AB |
| x02 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
∵-
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
∴0≤
| AD |
| AB |
| 3 |
| AD |
| AB |
| 3 |
（3）①当过准圆上点P的直线l与椭圆相切且其中一条直线的斜率为0而另一条斜率不存在时，则点P为(±
| 3 |
②当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，设点P（x0，y0），直线l的方程为m（y-y0）=x-x0．
联立
|
(3+m2)y2+(2mx0-2m2y0)y+m2y02+x02-2mx0y0-3=0，
∴△=(2mx0-2m2y0)2-4(3+m2)(m2y02+x02-2mx0y0-3)=0，
化为(y02-1)m2-2mx0y0+x02-3=0，
∵y02-1≠0，m存在，∴m1m2=
| x02-3 |
| y02-1 |
∵点P在准圆上，∴x02+y02=4，∴x02-3=1-y02，
∴m1m2═-1．
即直线l1，l2的斜率kl1•kl2=-1，因此当过准圆上的点P的直线l的斜率存在不为0且与椭圆相切时，直线l1⊥l2．
综上可知：在椭圆C的“准圆”上任取一点P，过点P作直线l1，l2，使得l1，l2与椭圆C都只有一个交点，l1⊥l2．
练习册系列答案
相关题目