题目内容
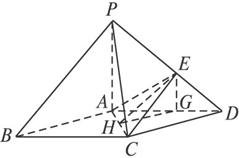
如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PB=PD=(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(3)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
思路解析:本小题主要考查了棱锥、直线与平面垂直的判定与性质,二面角及二面角的平面角、直线与平面平行的判定和性质,同时考查了利用空间向量解决立体几何问题的转换能力、一定的计算能力以及逻辑推理能力.
第(3)问在设问上有一定的开放性,这对空间观念的要求,对空间图形转换要求,在水平层次上就有较大的提高,切入点是从特殊点开始进行探究.
此题可用空间向量法解决,关键是能合理地构建空间坐标系.
总之,本题在解决方法上利用向量手段解决几何问题,很好地体现了数学的和谐美.同时,空间向量在立体几何中的应用为考生创造了几何证明的新思路,体现了解决问题策略的多样化.另外,本题通过开放性问题的设计,给学生留出了较大的思维空间,为学生灵活运用所学知识解决问题建立了一个平台.
(1)证明:因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a.
在△PAB中,由PA2+AB2=2a2=PB2,知PA⊥AB.同理,PA⊥AD.所以PA⊥平面ABCD.
(2)解:作EG∥PA交AD于G,由PA⊥平面ABCD,知EG⊥平面ABCD.

作GH⊥AC于H,连结EH.
则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE∶ED=2∶1,所以EG=![]() a,AG=
a,AG=![]() a,EH=AGsin60°=
a,EH=AGsin60°=![]() a.
a.
从而tanθ=![]() =
=![]() ,θ=30°.
,θ=30°.
(3)证明:当F是棱PC的中点时,BF∥平面AEC,证明如下:
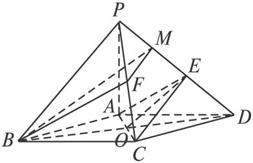
取PE的中点M,连结FM,则FM∥CE. ①
由EM=![]() PE=ED,知E是MD的中点.
PE=ED,知E是MD的中点.
连结BM、BD,设BD∩AC=O,则O为BD的中点.所以BM∥OE. ②
由①②知,平面BFM∥平面AEC.

 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2. 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2