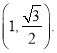Question

【题目】已知函数f（x）=ax2﹣2ax+b（a＞0）在区间[﹣1，4]上有最大值10和最小值1．设g（x）= ．
（1）求a、b的值；
（2）证明：函数g（x）在[ ，+∞）上是增函数；
（3）若不等式g（2x）﹣k2x≥0在x∈[﹣1，1]上有解，求实数k的取值范围．

Answer 1

【答案】
（1）解：f（x）=a（x﹣1）2﹣a+b，（a＞0），

因为a＞0，故 ，解得

（2）证明：由已知可得g（x）=x+ ﹣2，设 ≤x1＜x2，

∵g（x1）﹣g（x2）=（x1﹣x2）（1﹣ ）=

∵ ≤x1＜x2，∴x1﹣x2＜0，2＜x1x2，即x1x2﹣2＞0．

∴g（x1）﹣g（x2）＜0，即g（x1）＜g（x2）．

所以函数g（x）在[ ，+∞）上是增函数

（3）解：g（2x）﹣k2x≥0可化为2x+ ﹣2≥k2x，

化为1+2 ﹣2 ≥k，

令t= ，则k≤2t2﹣2t+1，

因x∈[﹣1，1]，故t∈[ ，2]，

记h（t）=2t2﹣2t+1，因为t∈[ ，2]，故h（t）max=5，

所以k的取值范围是（﹣∞，5]

【解析】（1）根据函数的对称轴得到关于a的方程组，解出即可；（2）先求出g（x）的表达式，根据定义证明函数的单调性即可；（3）问题转化为1+2 ﹣2 ≥k，令t= ，则k≤2t2﹣2t+1，构造新函数，结合函数的单调性从而求出k的范围即可．
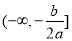【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较，以及对二次函数的性质的理解，了解当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．