题目内容
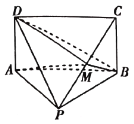
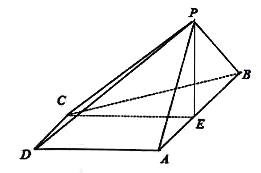
【题目】已知多面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
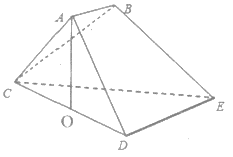
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)取CE中点F,连接BF,OF,由几何关系可证得四边形ABFO为平行四边形,结合线面平行的性质定理可得题中的结论;
(Ⅱ)取DE中点M,连接AF,由题意可证得ABEM为平行四边形,从而∠CAM或其补角为AC与BE所成的角.求得三角形的边长,利用余弦定理可得异面直线AC和BE所成角的余弦值.
(Ⅲ)由题意结合(Ⅱ)中的结论可知∠DBF就是直线BD与平面BEC所成角,利用边长的比值关系可得![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)取CE中点F,连接BF,OF,
∵O为CD的中点,
∴OF∥DE,且OF=DE,
∵AB//DE,AC=AD=CD=DE=2,AB=1,
∴OF∥AB,OF=AB,
则四边形ABFO为平行四边形,
∴AO//BF,BF平面BCE,AO平面BCE,
∴AO//平面BCE;
(Ⅱ)取DE中点M,连接AF,
∵AB∥DE,AB=1,DE=2,
∴AB∥ME,AB=ME ,
∴ABEM为平行四边形.
∴AM//BE.
∴∠CAM或其补角为AC与BE所成的角.
∵DE⊥平面ACD,AD,CD平面ACD,
∴DE⊥CD,DE⊥AD,
在![]() 中,CD=2,DM=1,
中,CD=2,DM=1,![]() ,
,
在![]() 中,AD=2,DM=1,
中,AD=2,DM=1,![]() ,
,
![]() .
.
所以异面直线AC和BE所成角的余弦值为![]() .
.
(Ⅲ)由题意可得BF//AO,
∵AO⊥平面CDE,∴BF⊥平面CDE,∴BF⊥DF.
∵CD=DE,∴DF⊥CE,
∵BF∩CE=F,∴DF⊥平面CBE;
∴∠DBF就是直线BD与平面BEC所成角.
在△BDF中,![]() ,
,
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目