题目内容
4.已知log2(logx5)=1,则x=$\sqrt{5}$.分析 由已知得logx5=2,化对数式为指数式,然后开方求得x值.
解答 解:由log2(logx5)=1,得logx5=2,化对数式为指数式得,x2=5,
∵x>0,∴x=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查指数式与对数式的互化,考查方程根的求法,是基础题.

练习册系列答案
相关题目
3.设方程log2x-($\frac{1}{2}$)x=0,log${\;}_{\frac{1}{2}}$x-($\frac{1}{2}$)x=0的根分别为x1、x2,则( )
| A. | x1x2=1 | B. | 0<x1x2<1 | C. | 1<x1x2<2 | D. | x1x2≥2 |
7.已知x,y满足不等式组$\left\{\begin{array}{l}{x≤2}\\{y≤3}\\{x+y≥2}\end{array}\right.$.则z=2x+y的取值范围为( )
| A. | [-1,3] | B. | [1,7] | C. | [1,3] | D. | [1,5] |
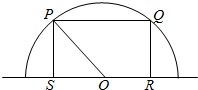 如图是半径为1的半圆,且PQRS是半圆的内接矩形,设∠SOP=α,则其值为$\frac{π}{4}$时,矩形的面积最大,最大面积为1.
如图是半径为1的半圆,且PQRS是半圆的内接矩形,设∠SOP=α,则其值为$\frac{π}{4}$时,矩形的面积最大,最大面积为1.