题目内容

直线L：
x
4
+
y
3
=1与椭圆E：
x2
16
+
y2
9
=1相交于A，B两点，该椭圆上存在点P，使得△PAB的面积等于3，则这样的点P共有（　　）
A．1个B．2个C．3个D．4个
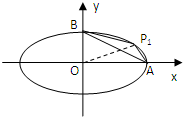
设P1（4cosα，3sinα）（0＜α＜
π
2
），即点P1在第一象限的椭圆上，考虑四边形P1AOB面积S，
S=S△OAP1+S△OBP1=
1
2
×4（3sinα）+
1
2
×3（4cosα）=6（sinα+cosα）=6
2
sin（α+
π
4
），∴Smax=6
2
．
∵S△OAB=
1
2
×4×3=6为定值，
∴S△P1AB的最大值为6
2
-6．
∵6
2
-6＜3，
∴点P不可能在直线AB的上方，显然在直线AB的下方有两个点P，
故选B．
练习册系列答案
相关题目
已知点F是双曲线C：x2-y2=2的左焦点，直线l与双曲线C交于A、B两点，
（1）若直线l过点P（1，2），且
OA
+
OB
=2
OP
，求直线l的方程．
（2）若直线l过点F且与双曲线的左右两支分别交于A、B两点，设
FB
=λ
FA
，当λ∈[6，+∞）时，求直线l的斜率k的取值范围．
已知A（-3，0），B（3，0）．若△ABC周长为16．
（1）求点C轨迹L的方程；
（2）过O作直线OM、ON，分别交轨迹L于M、N点，且OM⊥ON，求S△MON的最小值；
（3）在（2）的前提下过O作OP⊥MN交于P点．求证点P在定圆上，并求该圆的方程．
已知F1，F2为双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点．
（Ⅰ）若点P为双曲线与圆x2+y2=a2+b2的一个交点，且满足|PF1|=2|PF2|，求此双曲线的离心率；
（Ⅱ）设双曲线的渐近线方程为y=±x，F2到渐近线的距离是
2
，过F2的直线交双曲线于A，B两点，且以AB为直径的圆与y轴相切，求线段AB的长．
已知点D（0，-2），过点D作抛物线C1：x2=2py（p＞0）的切线l，切点A在第二象限，如图
（Ⅰ）求切点A的纵坐标；
（Ⅱ）若离心率为
3
2
的椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若k1+2k2=4k，求椭圆方程．
已知椭圆C的中心在原点，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|=2，点（1，
3
2
）在椭圆C上．
（1）求椭圆C的方程；
（2）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为
12
2
7
，求直线l的方程．
已知直线y=a交抛物线y=x2于A，B两点，若该抛物线上存在点C，使得∠ACB为直角，则a的取值范围为______．
设抛物线C1：y2=4mx（m＞0）的准线与x轴交于F1，焦点为F2，以F1，F2为焦点，离心率为
1
2
的椭圆C2与抛物线C1的一个交点为P．
（1）若椭圆的长半轴长为2，求抛物线方程；
（2）在（1）的条件下，直线l经过椭圆C2的右焦点F2，与抛物线C1交于A1，A2两点，如果|A1A2|等于△PF1F2的周长，求l的斜率；
（3）是否存在实数m，使得△PF1F2的边长是连续的自然数？若存在，求出m的值，若不存在，说明理由．
已知抛物线C的顶点在坐标原点，焦点在x轴上，抛物线C上的点M（2，m）到焦点F的距离为3．
（Ⅰ）求抛物线C的方程：
（Ⅱ）过点（2，0）的直线l与抛物线C交于A、B两点，若|AB|=4
6
，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网