题目内容
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).

(1)A类工人中和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表一
生产能力分组 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
人数 | 4 | 8 |
| 5 | 3 |
表二
生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
人数 | 6 |
| 36 | 18 |
①先确定![]() 再补全下列频率分布直方图(用阴影部分表示).
再补全下列频率分布直方图(用阴影部分表示).
②就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
③分别估计![]() 类工人生产能力的平均数和中位数(求平均数时同一组中的数据用该组区间的中点值作代表).
类工人生产能力的平均数和中位数(求平均数时同一组中的数据用该组区间的中点值作代表).
【答案】(1)25,75名;(2)①直方图见解析;②![]() 类工人中个体间的差异程度更小;③123,121.
类工人中个体间的差异程度更小;③123,121.
【解析】
(1)由分层抽样性质能求出![]() 类工人中和
类工人中和![]() 类工人中各抽查多少工人.
类工人中各抽查多少工人.
(2)①由频率分布表列出方程能求出补![]() ,
,![]() ,并补全下列频率分布直方图.
,并补全下列频率分布直方图.
②从频率分布直方图可以判断:![]() 类工人中个体间的差异程度更小.
类工人中个体间的差异程度更小.
③由频率分布直方图求出![]() 类工人生产能力的平均数和中位数.
类工人生产能力的平均数和中位数.
解:(1)由分层抽样性质得:
![]() 类工人中抽查:
类工人中抽查:![]() 名工人,
名工人,
![]() 类工人中抽查:
类工人中抽查:![]() 名工人.
名工人.
(2)①由题意得:![]() ,解得
,解得![]() .
.
![]() ,解得
,解得![]() .
.
补全频率分布直方图,如下图:
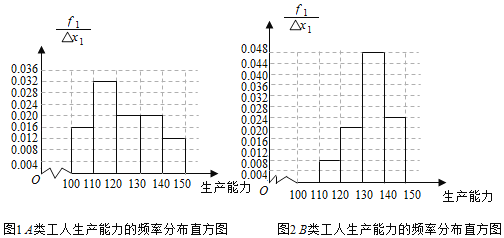
②从频率分布直方图可以判断:![]() 类工人中个体间的差异程度更小.
类工人中个体间的差异程度更小.
③![]() 类工人生产能力的平均数为:
类工人生产能力的平均数为:
![]() .
.
![]() 类工人生产能力的中位数的估计值为:
类工人生产能力的中位数的估计值为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】有编号为![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
编号 |
|
|
|
|
|
|
|
|
|
|
直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.51 | 1.47 | 1.46 | 1.53 | 1.47 |
其中直径在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)上述10个零件中,随机抽取1个,求这个零件为一等品的概率.
(2)从一等品零件中,随机抽取2个;
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率.