题目内容
【题目】设函数![]() .若方程
.若方程![]() 有且只有两个不同的实根,则实数
有且只有两个不同的实根,则实数![]() 的取值范围为 ( )
的取值范围为 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
对该题应用分类讨论思想分以下三种情况:
①若![]() 无实根,即
无实根,即![]() ,则不合题意.
,则不合题意.
②若![]() 有两个相等的实数根,此时
有两个相等的实数根,此时![]() 由
由![]() 得:
得:![]() ,无根,不合题意,故舍去.
,无根,不合题意,故舍去.
③若![]() 有两个不相等的实数根,也即
有两个不相等的实数根,也即![]() ,设
,设![]() 的实根为:
的实根为:![]() 和
和![]() ,则:方程
,则:方程![]()
![]() 或
或![]()
![]() 共有两个不等实根.进一步可知:方程
共有两个不等实根.进一步可知:方程![]()
![]() 和
和![]()
![]() 有且仅有一个方程有两个不等实根.即:
有且仅有一个方程有两个不等实根.即:![]() 和
和![]() 中一个方程有两不等实根另一个方程无实根.又由于
中一个方程有两不等实根另一个方程无实根.又由于![]() ,可得
,可得![]() ,
,![]() ,利用换元法解不等式可得
,利用换元法解不等式可得![]() 的取值范围。
的取值范围。
解:函数![]()
若方程![]() 有且只有两个不同的实根
有且只有两个不同的实根
①若![]() 无实根,即
无实根,即![]() ,则不合题意.
,则不合题意.
②若![]() 有两个相等的实数根,此时
有两个相等的实数根,此时![]() 由
由![]() 得:
得:![]() ,无根,不合题意,故舍去.
,无根,不合题意,故舍去.
③若![]() 有两个不相等的实数根,也即
有两个不相等的实数根,也即![]() ,设
,设![]() 的实根为:
的实根为:![]() 和
和![]() ,则:方程
,则:方程![]()
![]() 或
或![]()
![]() 有两个不等实根.进一步可知:方程
有两个不等实根.进一步可知:方程![]()
![]() 和
和![]()
![]() 有且仅有一个方程有两个不等实根.
有且仅有一个方程有两个不等实根.
即:![]() 和
和![]() 中一个方程有两不等实根另一个方程无实根.
中一个方程有两不等实根另一个方程无实根.
又由于![]() ,可得
,可得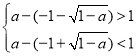 ,设
,设![]() ,则
,则![]()
则不等式组转化为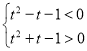 ,解得
,解得![]() ,
,
![]() ,
,![]()
即![]() 。
。
故选:A.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).

(1)A类工人中和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表一
生产能力分组 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
人数 | 4 | 8 |
| 5 | 3 |
表二
生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
人数 | 6 |
| 36 | 18 |
①先确定![]() 再补全下列频率分布直方图(用阴影部分表示).
再补全下列频率分布直方图(用阴影部分表示).
②就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
③分别估计![]() 类工人生产能力的平均数和中位数(求平均数时同一组中的数据用该组区间的中点值作代表).
类工人生产能力的平均数和中位数(求平均数时同一组中的数据用该组区间的中点值作代表).