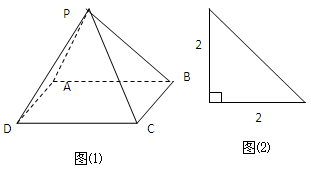
题目内容
如图所示,平面 ⊥平面
⊥平面 ,
,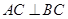 ,
,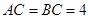 ,四边形
,四边形 是直角梯形,
是直角梯形,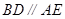 ,
,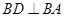 ,
, 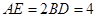 ,
,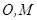 分别为
分别为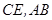 的中点.
的中点.

(Ⅰ) 用几何法证明: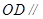 平面
平面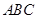 ;
;
(Ⅱ)用几何法证明: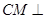 平面
平面 .
.
 ⊥平面
⊥平面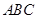 ,
,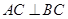 ,
,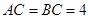 ,四边形
,四边形 是直角梯形,
是直角梯形,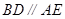 ,
,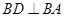 ,
, 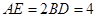 ,
,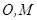 分别为
分别为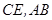 的中点.
的中点. 
(Ⅰ) 用几何法证明:
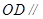 平面
平面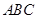 ;
;(Ⅱ)用几何法证明:
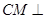 平面
平面 .
.(1)利用三角形的中位线的性质,先证明四边形ODBF是平行四边形,从而可得OD∥FB,利用线面平行的判定,可以证明OD∥平面ABC;(2)利用平面ABDE⊥平面ABC,证明BD⊥平面ABC,进而可证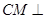 平面ABDE;
平面ABDE;
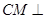 平面ABDE;
平面ABDE;试题分析:(Ⅰ)证明:取
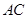 中点
中点 ,连结
,连结 . ∵
. ∵ 是
是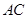 的中点,
的中点,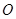 为
为 的中点,
的中点,∴
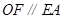 且
且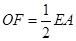 , 又
, 又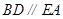 且
且 ,
,∴
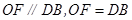 ,
,∴四边形
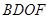 是平行四边形.
是平行四边形.∴
 4分
4分又∵
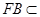 平面
平面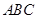 ,
,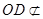 平面
平面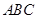 ,
,∴
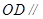 平面
平面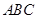 . 6分
. 6分(Ⅱ)证明:
 ,
,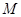 为
为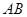 中点,∴
中点,∴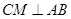 , 8分
, 8分又∵面
 ⊥面
⊥面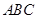 ,面
,面
 面
面 ,
,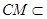 面
面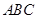 ,
,∴
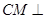 面
面 . 12分
. 12分点评:本题考查线面平行,考查线面垂直,考查线面角,解题的关键是正确运用线面平行与垂直的判定与性质,正确运用向量法求线面角.

练习册系列答案
相关题目
 中,
中,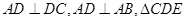 是边长为2的等边三角形,
是边长为2的等边三角形, .沿
.沿 将
将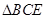 折起,使
折起,使 至
至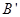 处,且
处,且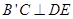 ;然后再将
;然后再将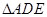 沿
沿 折起,使
折起,使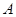 至
至 处,且面
处,且面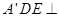 面
面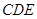 ,
,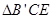 和
和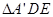 在面
在面

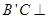 平面
平面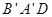 与平面
与平面
 与共面的直线m,n,下列命题为真命题的是 ( )
与共面的直线m,n,下列命题为真命题的是 ( )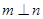 ,
, ,则
,则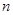 //
//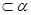 ,n//
,n//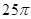
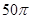

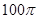
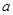 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与 和平面
和平面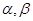 ,有如下四个命题:
,有如下四个命题: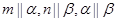 ,则
,则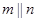 ;
;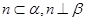 ,则
,则 ;
;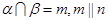 ,则
,则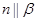 且
且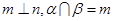 ,则
,则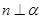 或
或 。其中真命题的个数是 .
。其中真命题的个数是 .