题目内容
已知直角梯形 中,
中, 是边长为2的等边三角形,
是边长为2的等边三角形, .沿
.沿 将
将 折起,使
折起,使 至
至 处,且
处,且 ;然后再将
;然后再将 沿
沿 折起,使
折起,使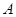 至
至 处,且面
处,且面 面
面 ,
, 和
和 在面
在面 的同侧.
的同侧.


(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求平面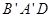 与平面
与平面 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
 中,
中, 是边长为2的等边三角形,
是边长为2的等边三角形, .沿
.沿 将
将 折起,使
折起,使 至
至 处,且
处,且 ;然后再将
;然后再将 沿
沿 折起,使
折起,使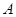 至
至 处,且面
处,且面 面
面 ,
, 和
和 在面
在面 的同侧.
的同侧.

(Ⅰ) 求证:
 平面
平面 ;
;(Ⅱ) 求平面
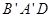 与平面
与平面 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.(Ⅰ)详见解析;(Ⅱ)平面 与平面
与平面 所构成的锐二面角的余弦值为
所构成的锐二面角的余弦值为 .
.
 与平面
与平面 所构成的锐二面角的余弦值为
所构成的锐二面角的余弦值为 .
.试题分析:(Ⅰ)在直角梯形ABCD中,由平面几何知识
 ,又
,又 ,可证得
,可证得 平面
平面 ;(Ⅱ)建立空间直角坐标系,利用法向量可求出二面角的余弦值.
;(Ⅱ)建立空间直角坐标系,利用法向量可求出二面角的余弦值.试题解析:(Ⅰ)证明:在直角梯形ABCD中,可算得

根据勾股定理可得
 ,即:
,即: ,又
,又 ,
, 平面
平面 ;
;(Ⅱ)以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,如图,则
 ,
, ,
, ,
, ,作
,作 ,因为面
,因为面 面
面 ,易知,
,易知, ,且
,且 ,
,从平面图形中可知:
 ,易知面CDE的法向量为
,易知面CDE的法向量为
设面PAD的法向量为
 ,且
,且 .
. 解得
解得
故所求平面
 与平面
与平面 所构成的锐二面角的余弦值为
所构成的锐二面角的余弦值为 .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.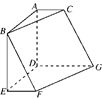
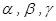 ,若
,若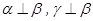 ,则
,则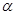 ∥
∥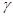 ;
;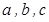 为三条两两异面的直线,则存在无数条直线与
为三条两两异面的直线,则存在无数条直线与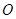 与棱长为
与棱长为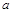 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为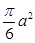 ;
;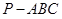 中,
中,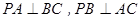 则
则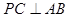 .
. 及其三视图中的主视图和左视图如图9所示,则棱
及其三视图中的主视图和左视图如图9所示,则棱 的长为_________.
的长为_________.
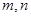 为不同的直线,
为不同的直线,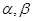 为不同的平面,给出下列四个命题:
为不同的平面,给出下列四个命题: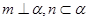 ,则
,则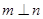 ; ②若
; ②若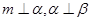 ,则
,则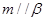 ;
;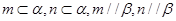 ,则
,则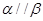 ; ④若
; ④若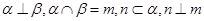 ,则
,则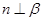 .
.  是空间的不同直线或不同平面,下列条件中能保证“若
是空间的不同直线或不同平面,下列条件中能保证“若 ,且
,且 ,则
,则 ”为真命题的是 ( )
”为真命题的是 ( ) 为直线,
为直线,  为平面
为平面 为直线,z为平面
为直线,z为平面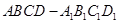 中,
中,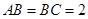 ,
,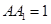 则
则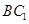 与平面
与平面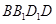 所成角的正弦值为 ( )
所成角的正弦值为 ( )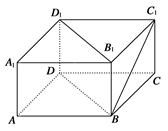




 ⊥平面
⊥平面 ,
, ,
, ,四边形
,四边形 ,
, ,
,  ,
, 分别为
分别为 的中点.
的中点. 
 平面
平面 平面
平面