题目内容
(本小题满分14分)
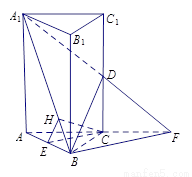
如图4,在三棱柱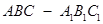 中,△
中,△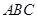 是边长为
是边长为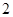 的等边三角形,
的等边三角形,
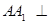 平面
平面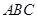 ,
,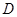 ,
,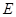 分别是
分别是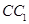 ,
,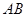 的中点.
的中点.
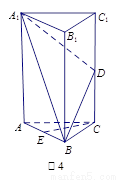
(1)求证: ∥平面
∥平面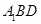 ;
;
(2)若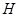 为
为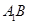 上的动点,当
上的动点,当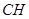 与平面
与平面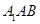 所成最大角的正切值为
所成最大角的正切值为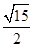 时,
时,
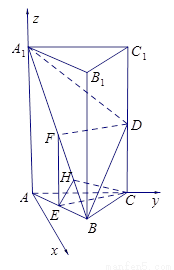
求平面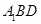 与平面
与平面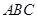 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
(1)延长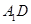 交
交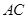 的延长线于点
的延长线于点 ,连接
,连接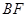 ∵
∵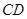 ∥
∥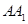 ,且
,且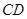
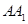 ∴
∴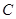 为
为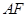 的中点. ∴
的中点. ∴ ∥
∥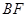 .∴
.∴ ∥平面
∥平面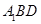 (2)
(2)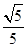
【解析】
试题分析:解法一:
(1)证明:延长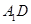 交
交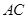 的延长线于点
的延长线于点 ,连接
,连接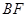 .
.
∵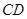 ∥
∥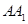 ,且
,且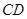
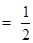
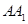 ,
,
∴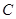 为
为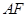 的中点.
的中点.
∵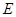 为
为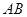 的中点,
的中点,
∴ ∥
∥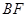 .
.
∵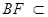 平面
平面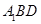 ,
,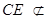 平面
平面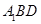 ,
,
∴ ∥平面
∥平面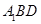 .
.
(2)解:∵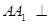 平面
平面 ,
,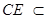 平面
平面 ,
,
∴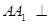
 .
.
∵△ 是边长为
是边长为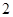 的等边三角形,
的等边三角形,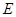 是
是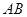 的中点,
的中点,
∴
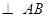 ,
,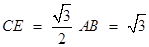 .
.
∵ 平面
平面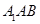 ,
,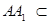 平面
平面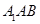 ,
,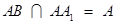 ,
,
∴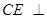 平面
平面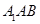 .
.
∴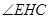 为
为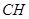 与平面
与平面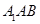 所成的角.
所成的角.
∵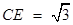 ,
,
在Rt△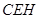 中,
中,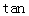
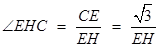 ,
,
∴当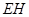 最短时,
最短时,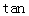
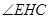 的值最大,则
的值最大,则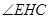 最大.
最大.
∴当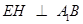 时,
时,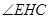 最大. 此时,
最大. 此时,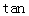
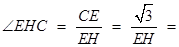
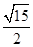 .
.
∴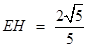 .
.
∵ ∥
∥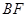 ,
,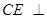 平面
平面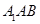 ,
,
∴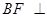 平面
平面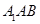 .
.
∵ 平面
平面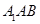 ,
,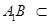 平面
平面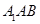 ,
,
∴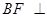
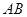 ,
,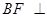
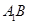 .
.
∴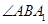 为平面
为平面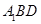 与平面
与平面 所成二面角(锐角).
所成二面角(锐角).
在Rt△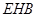 中,
中,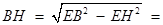
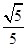 ,
,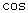
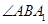
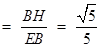 .
.
∴平面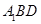 与平面
与平面 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为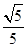 .
.
解法二:
(1)证明:取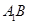 的中点
的中点 ,连接
,连接 、
、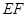 .
.
∵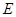 为
为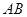 的中点,
的中点,
∴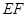 ∥
∥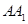 ,且
,且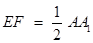 .
.
∵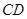 ∥
∥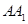 ,且
,且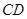
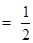
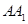 ,
,
∴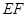 ∥
∥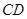 ,
,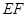
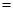
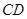 .
.
∴四边形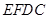 是平行四边形.
是平行四边形.
∴ ∥
∥ .
.
∵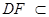 平面
平面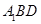 ,
,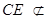 平面
平面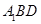 ,
,
∴ ∥平面
∥平面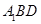 .
.
(2)解:∵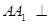 平面
平面 ,
,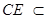 平面
平面 ,
,
∴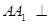
 .
.
∵△ 是边长为
是边长为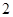 的等边三角形,
的等边三角形,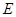 是
是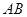 的中点,
的中点,
∴
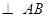 ,
,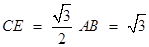 .
.
∵ 平面
平面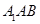 ,
,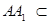 平面
平面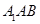 ,
,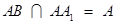 ,
,
∴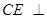 平面
平面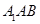 .
.
∴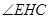 为
为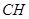 与平面
与平面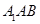 所成的角.
所成的角.
∵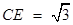 ,
,
在Rt△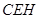 中,
中,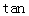
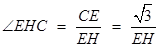 ,
,
∴当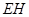 最短时,
最短时,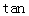
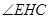 的值最大,则
的值最大,则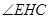 最大.
最大.
∴当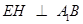 时,
时,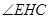 最大. 此时,
最大. 此时,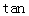
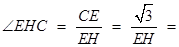
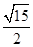 .
.
∴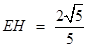 .
.
在Rt△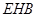 中,
中,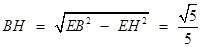 .
.
∵Rt△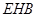 ~Rt△
~Rt△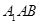 ,
,
∴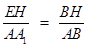 ,即
,即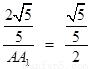 .
.
∴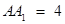 .
.
以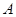 为原点,与
为原点,与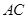 垂直的直线为
垂直的直线为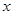 轴,
轴,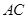 所在的直线为
所在的直线为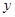 轴,
轴,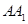 所在的直线为
所在的直线为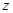 轴,
轴,
建立空间直角坐标系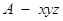 .
.
则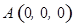 ,
,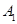
 ,
,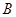
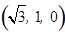 ,
,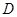
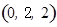 .
.
∴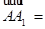
 ,
,
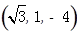 ,
,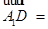
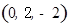 .
.
设平面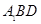 的法向量为
的法向量为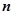
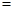
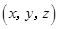 ,
,
由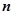
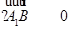 ,
,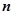
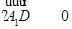 ,
,
得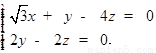
令 ,则
,则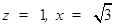 .
.
∴平面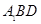 的一个法向量为
的一个法向量为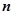
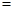
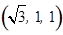 .
.
∵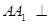 平面
平面 , ∴
, ∴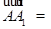
 是平面
是平面 的一个法向量.
的一个法向量.
∴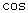

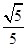 .
.
∴平面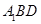 与平面
与平面 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为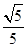 .
.
考点:线面平行的判定及线面角二面角
点评:立体几何题目若能找到从同一点出发的三线两两垂直则一般采用空间向量的方法求解,并且向量法求解立体几何问题是高考题目的方向。本题还考查了空间想象、推理论证、抽象概括和运算求解能力,以及化归与转化的数学思想方法

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)