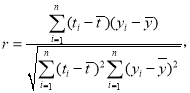题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)求出直线l的直角坐标方程为y![]() 2,曲线C是圆心为(
2,曲线C是圆心为(![]() ,1),半径为r的圆,直线l与曲线C相切,求出r=2,曲线C的普通方程为(x
,1),半径为r的圆,直线l与曲线C相切,求出r=2,曲线C的普通方程为(x![]() )2+(y﹣1)2=4,由此能求出曲线C的极坐标方程.
)2+(y﹣1)2=4,由此能求出曲线C的极坐标方程.
(2)设M(ρ1,θ),N(ρ2,![]() ),(ρ1>0,ρ2>0),由
),(ρ1>0,ρ2>0),由![]() 2sin(2
2sin(2![]() )
)![]() ,由此能求出△MON面积的最大值.
,由此能求出△MON面积的最大值.
(1)由题意可知将直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:![]() ;
;
可知曲线![]() 的方程为
的方程为![]() ,
,
![]() 曲线
曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设![]() ,
,![]() ,
,![]()
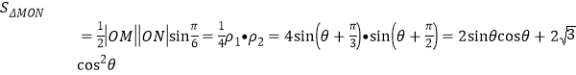
![]() .
.
当![]() 时,
时,![]() ,
,
![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目