题目内容
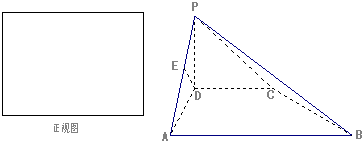
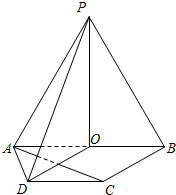
如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点
(1)求证:MN∥平面PAD;
(2)若∠PAD=45°,求证:MN⊥平面PCD.
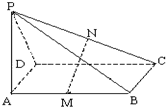
(1)求证:MN∥平面PAD;
(2)若∠PAD=45°,求证:MN⊥平面PCD.

(1)证明:取PD中点E,连结AE,EN,则有EN 平行且等于
CD,AM平行且等于
CD,
故有 EN和 AM平行且相等,∴AMNE为平行四边形,∴MN∥AE.
又AE?平面PAD,而 MN不在平面PAD内,所以MN∥平面PAD.-------(6分)
(2)∵PA⊥平面ABCD,AD?平面ABCD,∴PA⊥AD.
又∠PDA=45°,∴△PAD为等腰直角三角形.
又E是PD中点,∴AE⊥PD,又AE∥MN,∴MN⊥PD.
又ABCD为矩形,∴AB⊥AD.
又AB⊥PA,AD∩PA=A,∴AB⊥平面PAD.
∵AE?平面PAD,AB⊥AE,又AB∥CD,AE∥MN,∴MN⊥CD.
又∵PD∩CD=D,∴MN⊥平面PCD.…(12分)

| 1 |
| 2 |
| 1 |
| 2 |
故有 EN和 AM平行且相等,∴AMNE为平行四边形,∴MN∥AE.
又AE?平面PAD,而 MN不在平面PAD内,所以MN∥平面PAD.-------(6分)
(2)∵PA⊥平面ABCD,AD?平面ABCD,∴PA⊥AD.
又∠PDA=45°,∴△PAD为等腰直角三角形.
又E是PD中点,∴AE⊥PD,又AE∥MN,∴MN⊥PD.
又ABCD为矩形,∴AB⊥AD.
又AB⊥PA,AD∩PA=A,∴AB⊥平面PAD.
∵AE?平面PAD,AB⊥AE,又AB∥CD,AE∥MN,∴MN⊥CD.
又∵PD∩CD=D,∴MN⊥平面PCD.…(12分)


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目